Не следует путать с метрическим пространством — множеством, в котором определено расстояние между любой парой элементов.

Метри́ческий те́нзор или ме́трика — это симметричное тензорное поле ранга (0,2) на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т.

Доставка синих ромашек в Москве (Antananarivo)

д.

В частном случае поверхности метрика также называется первой квадратичной формой.

В общей теории относительности метрика рассматривается в качестве фундаментального физического поля (гравитационного) на четырехмерном многообразии физического пространства-времени. Широко используется и в других построениях теоретической физики, в частности, в биметрических теориях гравитации на пространстве-времени рассматривают сразу две метрики.

А для любых векторных полей скалярное произведение вычисляется по формуле

Например, риманов метрический тензор может быть задан ортонормированным полем реперов^[1].

Обычно под метрическим тензором без специального на то указания в математике понимается риманов метрический тензор; но если, рассматривая невырожденный метрический тензор, хотят подчеркнуть, что речь идет именно о римановом, а не псевдоримановом метрическом тензоре, то о нём говорят как о собственно римановом метрическом тензоре. В физике под метрическим тензором обычно подразумевают лоренцеву метрику пространства-времени.

Иногда под псевдоримановым тензором и псевдоримановым многообразием понимают то, что выше определено как собственно псевдоримановы метрика и многообразие, а для первых сохраняется только термин «невырожденная метрика» и соответственно «многообразие с невырожденной метрикой».

Интегрирование же по объему включает этот множитель, например, при необходимости проинтегрировать в координатах какой-то скаляр (чтобы результат был инвариантным):

Для тензорных полей это позволяет «поднимать и опускать индексы» у любого тензорного поля (жаргонное название — «жонглирование индексами»). В компонентах операция поднятия-опускания индекса, выглядит так:

Для тензороподобных объектов (не являющихся тензорами), как например символы Кристоффеля, преобразование контравариантных компонент в ковариантные и обратно определяется, как правило, так же, как и для тензорных. При желании жонглирование можно применить и к матрицам Якоби, только в этом случае нужно проследить за тем, что метрика для поднятия-опускания первого индекса будет, конечно, вообще говоря, отличаться от метрики для такой же операции со вторым.

ТЕНЗОРЫ

Понятие тензора (от латинского tendo — напрягаю, растягиваю) принадлежит к числу основных, фундаментальных математических понятий и широко применяется сейчас в механике, электродинамике, теории относительности и т. д. Первоначально возникшее в рабо­тах XIX века по теории упругости, оно было систематически иссле­довано в 1886 —1901 гг. итальянским геометром Г. Рйччи-Курбастро (1853—1925) и итальянским математиком и механиком Т. Лёви-Чивйта (1873—1942).

 

 

Внимание к новому аппарату существенно возросло после создания в 1915 —1916 гг. великим ученым, физиком А. Эйнштейном (1879 — 1955) общей теории относительности, мате­матическая часть которой целиком основана на тензорном исчислении. Физические величины, которые нам встре­чались до сих пор, были либо скалярными, либо векторными. Однако существуют физические величины более сложной природы.

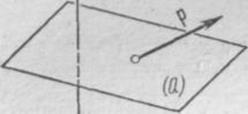
Например, однородное напряженное состоя­ние упругого тела характеризуется плотностью р силы, с которой одна часть тела действует на другую через мысленно вы­деленную плоскость (Q) (рис.

Antananarivo

1); однако при этом р для различных направлений плоскости (Q) будет различным. Таким образом, вели­чина, характеризующая напряженное состояние, уже не является вектором, она представляет собой тензор 2-го ранга.

Оказывается, что и многие другие важные величины, характеризующие состояние сплошных сред, также являются тен­зорами.

К настоящему времени тензорная алгебра, а также тензорный анализ (т. е. теория тензорных полей, связанная с применением диф­ференцирования и интегрирования) представляют собой значительно разработанные дисциплины.

 

§ 1. Тензорная алгебра

1. Примеры.К понятию тензора можно прийти уже размышляя над описанием векторов в обычном пространстве с помощью чисел. Как известно из векторной алгебры, все действия над векторами удобно осуществлять, выбрав евклидов базис i, j, k, после чего можно любой вектор а разложить по этому базису

а = а_хi + а_уj+ a_zk (1)

и взамен действий над векторами осуществлять действия над их про­екциями, т. е. над числами — коэффициентами разложений. Более того, даже задавать конкретные векторы обычно бывает удобнее с помощью разложения (1), чем каким-то геометрическим способом.

Однако задумаемся теперь, что это за векторы i, j, k. В некото­рых случаях, когда в задаче имеется естественная система отсчета направлений (например, во многих задачах статики), эти векторы можно описать вполне точно, «привязав» их к данным задачи. Но во многих случаях привлечение такой «абсолютной» системы отсчета является весьма искусственным либо вообще невозможно. Тогда по­лучается на первый взгляд парадокс: мы пользуемся проекциями вполне определенного вектора, которые зависят от выбора базиса, но не уточняем, как этот базис выбирается…

Эта трудность будет преодолена, если с самого начала отка­заться от выбора какого-то одного базиса, а считать, что все ба­зисы равноправны и каждому выбору базиса i, j, k отвечает на­бор значений а_х, а_у, а_zв соответствии с формулой (1). Подобный набор величин, приобретающих определенные значения лишь после выбора базиса и преобразующихся по определенному правилу при за­мене базиса (см. ниже), и называется тензором (или тензорной вели­чиной), а сами эти величины, составляющие в определенном порядке тензор, называются его компонентами. (Отметим некоторое несо­ответствие: в векторной алгебре принято компонентами вектора A называть в е к торы а_хi, а_уj, a_zk. Однако здесь мы будем компонентами называть величины а_х, а_y , а_z.)

В тензорном исчислении принято не писать знак суммы по повто­ряющемуся индексу, а при повторении индекса всегда осуществлять такое суммирование, т. е. писать последнюю формулу.

Здесь индекс суммирования является немым и может быть обозна­чен любой буквой, а пределы суммирования определяются размер­ностью пространства, в котором рассматривается тензор.

 

Напряженное состояние в окрестности точки

Если через произвольную точку тела провести три взаимно перпендикулярные площадки параллельно координат­ным плоскостям, то девять составляющих (компонент) напря­жения: три нормальных а_х, а_у, ст_г и шесть касательных х_ху, т,₂, т_2Х, т_ух, t_xz, х_zy, действующих на этих площадках (рис. 4.1),

полностью определяют напряженное состояние в окрестности данной точки. Это означает, что, зная эти девять величин, можно найти напряжения на любой наклонной площадке, проходя­щей через данную точку. Слово «со­ставляющая» или «компонента» в дальнейшем для краткости будем опускать.

Все девять напряжений можно обозначить одинаково, например, Gij{hj=x, У, z). Тогда при г’=у получа­ются нормальные напряжения, в которых сохраняется только один индекс, а при i Ф]—касательные напряжения. Первый индекс указывает, параллельно какой оси направлено напряже­ние, а второй обозначает нормаль к площадке, на которой оно действует. Это правило непосредственно относится к касатель­ным напряжениям, но им также можно пользоваться и для нормальных напряжений, если употреблять обозначения <у_и.

Нормальные напряжения считаются положительными, если они направлены в сторону внешней Нормали к площадке, и наоборот. В соответствии с этим правилом положительные нормальные напряжения считаются растягивающими, а от­рицательные — сжимающими.

Для касательных напряжений принимается следующее правило знаков. На площадке, внешняя нормаль к которой направленав положительном (или отрица­тельном) направлении соответст­вующей оси, касательное напряже­ние считается положительным, ес­ли оно также направлено в поло­жительном (или отрицательном) направлении оси. На рис. 4.1 пока­заны положительные напряжения.

Проведем вблизи точки О тела произвольную наклонную площад­ку ABC, площадь которой обозна­чим через dF(рис. 4.2). Положение этой площадки может быть опреде­лено углами, которые составляет нормаль v с осями координат.

Как известно из аналитической геометрии, направляющие косинусы нормали связаны между собой соотношением

l² + m²+n² = 1. (4.1)

Полное напряжение p_v, действующее на этой площадке, можно спроектировать на оси координат. Проекции p_xv, p_yv, p_zv определяются из уравнений равновесия тетраэдра ОАВС. Составим сумму проекций всех сил, приложенных к граням тетраэдра, на ось Ох (на рис. 4.2 на вертикальных и горизон­тальной гранях тетраэдра показаны только те напряжения, которые дают проекции на ось

123

ПОСМОТРЕТЬ ЕЩЕ:

Государственный комитет Российской Федерации
по высшему образованию
Нижегородский государственный университет
им. Н.И. Лобачевского

УЧЕБНАЯ ПРОГРАММА

по общему курсу

ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА

для направления подготовки
"физика"
и по специальности
"радиофизика и электроника"

Курс: 2
Семестр: 3
Лекции: 54 час.
Практикум: 36 час.
Экзамен: 3 семестр

 

Программа составлена
профессором кафедры математики радиофизического факультета Нижегородского государственного университета д. ф.-м. н. А.И. Саичевым, доцентом кафедры математики к. ф.-м. н. В.Н. Кошелевым.

Н.Новгород 1995

ЦЕЛИ И ЗАДАЧИ КУРСА

ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА

1. Учебные цели курса.

Курс "Основы векторного и тензорного анализа" предполагает знакомство студентов радиофизического факультета с математическим и обьектами, составляющими необходимую и важную часть языка теоретической физики, классической и квантовой механики, теории электромагнитного поля и др. Этот раздел блока "Высшая математика" наиболее богат физическими приложениями, связанными в частности с практическим применением формул Стокса и Остроградского, дифференциальных операторов в ортогональных криволинейных координатах. В разделе "Элементы дифференциальной геометрии" закладываются знания, необходимые для курса "Классическая механика".

2. Учебные задачи курса.

Научить студентов свободно владеть дифференциальными операциями теории поля, необходимыми при дальнейшем изучении теоретических курсов физики. Ознакомить студентов с глобальными понятиями теории поля: поток, циркуляция и т.д. Научить вычислять эти величины, используя поверхностные и криволинейные интегралы, некоторые понятия дифференциальной геометрии. Введя понятие тензора, подготовить студентов к дальнейшему изучению тензорных полей.

3. Дисциплины, изучение которых необходимо для изучения курса.

Для изучения курса "Основы векторного и тензорного анализа" нужно знать следующие разделы курса "Математический анализ": диференциальное и интегральное исчисление функций одной и многих переменных, а также курсы "Аналитическая геометрия и высшая алгебра" и "Дифференциальные уравнения".

СОДЕРЖАНИЕ КУРСА

"ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА"

(наименование тем и их содержание)

1. Векторные функции. 4 часа.

1.1. Предел и непрерывность векторной функции.

1.1.1. Понятие векторной функции одной и нескольких переменных.

1.1.2. Предел векторной функции. Свойства пределов векторных функций.

1.1.3. Непрерывность векторной функции.

1.2. Дифференцируемые функции.

1.2.1. Дифференцирование векторной функции одной переменной.

1.2.2. Геометрический смысл производной векторной функции.

1.2.3. Дифференцирование векторной функции многих переменных.

1.2.4. Дифференциал векторной функции многих переменных.

1.2.5. Производные по направлению от скалярной и векторной функции.

1.2.6. Вычисление производной по направлению.

1.2.7. Формула Тейлора для векторной функции.

1.3. Интегрирование векторных функций.

1.3.1. Определения интегралов от векторных функций.

1.3.2. Свойства интегралов от векторных функций.

1.3.3. Интегральная теорема о среднем.

2. Элементы дифференциальной геометрии. 12 часов.

2.1. Пространственные кривые.

2.1.1. Основной трехгранник кривой.

2.1.2. Формулы Френе.

2.1.3. Вычисление кривизны и кручения.

2.1.4. Система координат, связанная с основным трехгранником.

2.1.5. Уравнения касательной, главной нормали, бинормали, нормальной плоскости.

2.1.6. Ориентированная кривизна плоской кривой.

2.2. Дифференциальная геометрия на поверхности.

2.2.1. Понятие поверхности. Параметризация поверхности. Простая поверхность. Гладкая поверхность.

2.2.2. Нормаль и касательная плоскость к поверхности.

2.2.3. Системы координат в касательных плоскостях.

2.2.4. Измерение на кривой поверхности длин, углов и площадей.

2.2.5. Первая квадратичная форма поверхности. Кривизна линии на поверхности.

2.2.6. Вторая квадратичная форма поверхности.

3. Поверхностные интегралы. 8 часов.

3.1. Поверхностный интеграл 1-го типа.

3.1.1. Определение, физический смысл.

3.1.2. Вычисление площади гладкой поверхности.

3.1.3. Вычисление поверхностного интеграла первого типа.

3.2. Поверхностный интеграл 2-го типа.

3.2.1. Односторонние и двухсторонние поверхности.

3.2.2. Определение поверхностного интеграла 2-го типа.

3.2.3. Физический смысл поверхностного интеграла 2-го типа.

3.2.4. Вычисление поверхностного интеграла 2-го типа.

3.2.5. Формула Гаусса-Остроградского.

3.2.6. Формула Стокса.

4. Теория поля. 20 часов.

4.1.Скалярное поле.

4.1.1. Определение скалярного поля Поверхность уровня и ее основные свойства.

4.1.2. Производная по обьему от функции области.

4.1.3. Градиент: инвариантное определение, вычисление в декартовых прямоугольных координатах.

4.1.4. Свойства градиента.

4.2. Векторное поле.

4.2.1. Определение векторного поля. Примеры.

4.2.2. Векторные линии. Задача о нахождении векторной линии.

4.2.3. Векторная трубка.

4.2.4. Поток векторного поля.

4.2.5. Дивергенция: инвариантное определение, физический смысл, вычисление в декартовых прямоугольных координатах.

4.2.6. Инвариантный вид формулы Остроградского.

4.2.7. Ротор: инвариантное определение, физический смысл, вычисление в декартовых прямоугольных координатах.

4.3. Оператор Гамильтона (вектор "набла").

4.3.1. Общая теорема Гаусса-Остроградского, записанная с помощью вектора "набла".

4.3.2. Действия с вектором "набла".

4.3.3. Дифференциальные операторы, порождаемые вектором "набла"

4.4. Специальные виды полей.

4.4.1 Потенциальное поле. Скалярный потенциал и его свойства.

4.4.2. Циркуляция векторного поля. Инвариантный вид формулы Стокса.

4.4.3.Соленоидальное поле. Векторный потенциал и его свойства

4.4.4. Лапласово поле.

4.4.5. Основная теорема векторного анализа.

4.5. Дифференциальные операции второго порядка.

4.6. Дифференциальные операции теории поля в криволинейных координатах.

4.6.1. Основной и взаимный базисы.

4.6.2. Ковариантные и контравариантные координаты.

4.6.3. Криволинейные координаты в пространстве.

4.6.4. Локальный базис и локальный взаимный базис.

4.6.5. Ортогональные криволинейные координаты. Условие ортогональности криволинейных координат.

4.6.6. Элемент длины в ортогональных криволинейных координатах. Коэффициенты Ламе.

4.6.7. Градиент, дивергенция, ротор, оператор Лапласа в ортогональных криволинейных координатах.

5. Тензоры. 12 часов.

5.1. Аффинный ортогональный тензор.

5.1.1. Преобразование ортонормированных базисов.

5.1.2. Определение афинного ортогонального тензора. Примеры.

5.1.3. Алгебраические действия над афиннными ортогональными тензорами.

5.2. Тензоры в афинных координатах.

5.2.1. Тензорная символика. Понятие тензора любого строения.

5.2.2. Тензорная алгебра: сложение, умножение тензоров, свертка, перестановка индексов, симметрирование, альтернация,метрический тензор, подъем и опускание индексов.

5.2.3. Обратный тензорный признак.

5.2.4. Псевдотензоры.

5.2.5. Понятие тензорного поля. Дифференциальные операции тензорного поля.

Основная литература

1. Будак Б.М., Фомин С.В., Кратные интегралы и ряды, М.: Наука, 1967.
2. Кочин Н.Е., Векторное исчисление и начала тензорного исчисления, ГОНТИ, 1938.

Дополнительная литература

1. Арфкен Г., Математические методы в физике, М.: Атомиздат, 1970.
2. Гольдфайн И.А., Векторный анализ и теория поля, М.: Наука, 1968.
3. Рашевский П.К., Риманова геометрия и тензорный анализ, М.:
4. Наука, 1964.
5. Джефферс Г., Свирлс Б., Методы математической физики, т.1, М.: Мир, 1969.

ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ.

3 СЕМЕСТР (36 часов на 1 группу)

1.

Поверхностные интегралы — 14 часов.

1.1. Поверхностные интегралы 1-го типа (4 часа).

1.2. Поверхностные интегралы 2-го типа (4 часа).

1.3. Формула Стокса (2 часа).

1.4. Формула Остроградского (2 часа).

1.5. Контрольная работа по теме (2 часа).

2. Теория поля — 14 часов.

2.1. Основные понятия теории поля (8 часов).

2.2. Действия с вектором "набла" (4 часа).

2.3. Контрольная работа (2 часа).

3. Тензоры — 8 часов.

3.1. Тензоры (4 часа).

3.2. Физические приложения тензоров (4 часа).

ЛИТЕРАТУРА.

1. Демидович Б.П., Сборник задач и упражнений по математическому анализу, М.: Наука, 1972.
2. Мисюркеев И.В., Сборник задач по методам математической физики, М.: Просвещение, 1975.
3. Арфкен Г., Математические методы в физике, М.: Атомиздат, 1970.

ОБЗОР РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ ПО ТЕМАМ КУРСА

"ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА"

Тема 1. Векторные функции.

Основные вопросы темы изложены в учебниках [1] основной литературы и [4] дополнительной литературы.

Тема 2. Элементы дифференциальной геометрии.

Основные вопросы темы изложены в учебнике [1] основной литературы.

Тема 3. Поверхностные интегралы.

Основные вопросы темы изложены в учебнике [1] основной литературы.

Тема 4. Теория поля.

Основные вопросы темы изложены в учебниках [1] основной литературы и [3], [4], [6] дополнительной литературы.

Тема 5. Тензоры.

Основные вопросы темы изложены в учебниках [1], [2] основной литературы и [3], [5] дополнительной литературы.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ.

1. Определение векторной функции одного и многих переменных.

2. Определение предела векторной функции по Коши и по Гейне. Свойства пределов векторных функций.

3. Непрерывность векторной функции. Действие с непрерывными функциями.

4. Дифференцируемые функции (4 случая).

5. Дифференцирование векторной функции одной переменной (определение и две теоремы). . Геометрический смысл производной от векторной функции.

7. Определение частной производной векторной функции многих переменных. Теорема о существовании частных производных у дифференцируемой функции.

8. Определение производной по направлению. Теоремы о вычислении производных по направлению.

9.

Интегрирование векторных функций.

10. Основной трехгранник кривой.

11. Система координат связанная с основным трехгранником. Координатные линии и координатные плоскости. Уравнение касательной, нормами, бинормали, нормальной плоскости, спрямляемой плоскости и соприкасающейся плоскости.

12. Формулы Френе. Понятие кривизны и кручения кривой.

13. Вычисление величины кривизны и кручения.

14. Вид кривой вблизи произвольной ее точки.

15. Определение поверхности. Способы задания поверхности. Простая поверхность, гладкая поверхность.

16. Нахождение нормали и касательной плоскости к поверхности.

17. Вычисление направляющих косинусов нормали к поверхности.

18. Длина кривой на поверхности. Первая квадратичная форма поверхности.

19. Определение площади гладкой поверхности. Теорема о вычислении площади гладкой поверхности. Следствия.

20. Нормальные сечения поверхности и их кривизна. Вторая квадратичная форма.

21. Определение поверхностного интеграла 1-го типа. Теорема о вычислении.

22. Вывод формулы Остроградского.

23. Вывод формулы Стокса.

24. Односторонние и двусторонние поверхности. Сторона поверхности.

Определение поверхностного интеграла 2-го типа. Теорема о вычислении.

25. Определения: скалярное поле, поверхность уровня (ее свойства), предел функции от области, производная по объему (ее физический смысл).

26. Определение градиента скалярного поля. Теорема о вычислении. Следствие.

27. Свойства градиента.

28. Определение векторного поля. Векторная линия. Задача о нахождении векторной линии. Векторная трубка. Поток векторного поля. Векторный поток.

29. Дивергенция векторного поля. Теорема о вычислении. Инвариантный вид формулы Остроградского. Физический смысл дивергенции и формулы Остроградского.

30. Определение ротора векторного поля. Теорема о вычислении. Следствие.

31. Физический смысл ротора.

32. Оператор Гамильтона. Действия с вектором "набла". Дифференциальные операторы, порожденные вектором "набла".

33. Общая теорема Гаусса-Остроградского.

34. Потенциальное поле. Теорема о вычислении потенциала. Критерий потенциальности поля.

35. Циркуляция векторного поля. Инвариантный вид формулы Стокса.

36. Соленоидальное поле. Критерий соленоидальности поля. Свойства соленоидального поля.

37. Лапласово поле. Основная теорема векторного анализа ( без доказательства ). Дифференциальные операции второго порядка.

38. Основной и взаимный базисы. Ковариантные и контравариантные координаты вектора.

39. Определение криволинейных координат в пространстве. Координатные линии и координатные поверхности. Теорема о нахождении локальных базисов (основного и взаимного).

40. Определение ортогональных криволинейных координат. Критерий ортогональности. Элемент длины. Коэффициенты Ламе.

41. Вывести формулы в ортогональных криволинейных координатах для градиента и оператора Лапласа.

42.

Дивергенция в ортогональных криволинейных координатах.

43. Ротор в ортогональных криволинейных координатах.

44. Дифференциальные операции теории поля в сферических координатах

45. Дифференциальные операции теории поля в цилиндрических координатах.

46. Преобразования ортонормированных базисов.

47. Определение аффинного ортогонального тензора. Примеры: вектор, поверхность.

48. Линейный оператор в векторном пространстве как аффинный ортогональный тензор.

49. Тензорная символика.

50. Преобразование косоугольных базисов.

51. Общее определение тензора. Примеры.

52. Метрический тензор.

53. Тензорная алгебра. Сложение. Умножение. Свертка. Перестановка индексов. Симметрирование. Альтернация. Подъем и опускание индексов.