admin / 12.11.2018
Матрица поворота в трехмерном пространстве
.
Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в трёхмерном пространстве
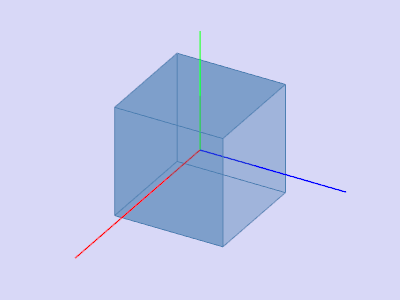
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x: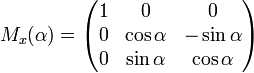
Вращение вокруг оси y: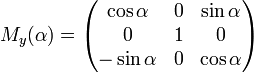
Вращение вокруг оси z:
После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;
По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);
По оси Z
x’=x*cos(L)-y*sin(L);
y’=x*sin(L)+y*cos(L);
z’=z;
Все три поворота делаются независимо друг от друга, т.е.
Содержание
- Вращение в одной системе координат
- 6.Перенос и повороты в трехмерном пространстве.
- 3.2. Трехмерные преобразования и проекции
- Матрица вращения
- Матрица поворота
- План:
- Введение
- 1. Матрица вращения
- 2. Матрица поворота в трёхмерном пространстве
- 3. Свойства матрицы поворота
- Литература
- 6.Перенос и повороты в трехмерном пространстве.
Вращение в одной системе координат
если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Переход из одной прямолинейной координатной системы в трёхмерном пространстве к другой описывается в общем случае следующим образом:

или в матричном виде:

Рассмотрим матрицы, соответствующие следующим базовым геометрическим преобразованиям:
1. Повороты

- вокруг оси X на угол


- вокруг оси Y на угол


- вокруг оси Z на угол


2. Растяжение (сжатие):
 ,
,если
 — растяжение,
— растяжение,  — сжатие
— сжатие3. Отражение (зеркалирование)
- относительно плоскости XOY

- относительно плоскости YOZ

- относительно плоскости ZOX

4. Перенос (сдвиг, перемещение) на вектор 

Важно:преобразование точки (с сохранением расположения исходной системы координат) соответствует выполнению обратной операции по отношению к преобразованию системы координат. Например, поворот точки на некоторый угол по часовой стрелке вокруг оси X соответствует повороту системы координатпротив часовой стрелки на тот же угол.
Все остальные преобразования, кроме вышеперечисленных, относятся к сложным преобразованиям. Матрицы сложных преобразований получаются при помощи нахождения произведения матриц, соответствующих базовым геометрическим преобразованиям, которые необходимо осуществить для получения искомого сложного преобразования (*-умножение производится строго в том порядке, в котором эти базовые преобразования производятся, т.к. преобразования некоммутативны).
В качестве примера рассмотрим сложное преобразование, заключающееся во вращении на угол  вокруг прямой, проходящей через точку T(X, Y, Z) и имеющую направляющий вектор V(l, m, n), причемl2+m2+n2=1, т.е. вектор V является единичным.
вокруг прямой, проходящей через точку T(X, Y, Z) и имеющую направляющий вектор V(l, m, n), причемl2+m2+n2=1, т.е. вектор V является единичным.
Необходимо разложить преобразование на ряд элементарных шагов (базовых преобразований).
Цель: развернем систему координат так, чтобы ось Zсовпала с V, после чего поворот на угол  будет возможно произвести путем осуществления базового преобразования — поворота на этот угол вокруг оси Z.
будет возможно произвести путем осуществления базового преобразования — поворота на этот угол вокруг оси Z.
6.Перенос и повороты в трехмерном пространстве.
Для достижения этой цели выполним следующую последовательность базовых преобразований:
- Перенос вектора Vв начало координат:
- Поворот системы координат вокруг оси Zна угол
 вокруг оси X (т.к. разворачиваем «систему координат» по часовой стрелке, то это тоже самое, что разворот точки против часовой стрелки).
вокруг оси X (т.к. разворачиваем «систему координат» по часовой стрелке, то это тоже самое, что разворот точки против часовой стрелки). - Поворот системы координат вокруг оси ординат на угол

- Поворот вокруг Vна угол
 , а т.к. V совпадает с осью аппликат, то матрица этого преобразования имеет следующий вид:
, а т.к. V совпадает с осью аппликат, то матрица этого преобразования имеет следующий вид: - Поворот вокруг оси ординат на угол «
 » — [Ry]
» — [Ry] - Поворот вокруг оси абсцисс на угол «
 » — [Rx]
» — [Rx] - Перенос на вектор T(X, Y, Z).








А так как нам необходимо вернуться в исходную систему координат, то:
Перспективное изображение возникает при центральном проецировании, т.е. когда центр проецирования (глаз наблюдателя) находится на конечном расстоянии от экрана.
Матрица перспективного преобразования с проецированием на плоскость XOY:
 ,
,
где С(0, 0, c) — точка расположения наблюдателя (центр проецирования). Плоскость проецирования, т.е. экран, совпадает с координатной плоскостью XOY.
Назад | Оглавление | Домой | Далее
3.2. Трехмерные преобразования и проекции
Рассмотрим трехмерную декартовую систему координат, являющуюся правосторонней.
Матрица вращения
Примем соглашение, в соответствии с которым будем считать положительными такие повороты, при которых (если смотреть с конца полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:
|
Если ось вращения |
Положительным будет направление поворота |
|
X |
От y к z |
|
Y |
От z к x |
|
Z |
От x к y |

Рис. 3.6. Трехмерная система координат
Аналогично тому, как точка на плоскости описывается вектором (x,y), точка в трехмерном пространстве описывается вектором (x,y,z).
Как и в двухмерном случае, для возможности реализаций трехмерных преобразований с помощью матриц перейдем к однородным координатам:
[x,y,x,1] или [X,Y,Z,H]
[x*,y*,z*1] = [ ], где Н¹1, Н¹0.
], где Н¹1, Н¹0.
Обобщенная матрица преобразования 4´4 для трехмерных однородных координат имеет вид
| Т = |  |
Эта матрица может быть представлена в виде четырех отдельных частей:
 .
.
· Матрица 3´3 осуществляет линейное преобразование в виде изменения масштаба, сдвига и вращения.
· Матрица 1´3 производит перенос.
· Матрица 3´1- преобразования в перспективе.
· Скалярный элемент 1´1 выполняет общее изменение масштаба.
Рассмотрим воздействие матрицы 4´4 на однородный вектор [x,y,z,1]:
1.Трехмерный перенос – является простым расширением двумерного:
| T(Dx,Dy,Dz)= |  |
т.
е. [x,y,z,1]*T(Dx,Dy,Dz)=[x+Dx,y+Dy,z+Dz,1].
2.Трехмерное изменение масштаба.
Рассмотрим частичное изменение масштаба. Оно реализуется следующим образом:
| S(Sx,Sy,Sz)= |  |
т. е. [x,y,z,1]*S(Sx,Sy,Sz)=[Sx*x,Sy*y,Sz*z,1].
Общее изменение масштаба получается за счет 4-го диагонального элемента, т. е.
| [x y z 1] * |  |
= [x y z S] = [x* y* z* 1] = [ ]. ]. |
Такой же результат можно получить при равных коэффициентах частичных изменений масштабов. В этом случае матрица преобразования такова:
| S= |  |
3. Трехмерный сдвиг
Недиагональные элементы матрицы 3´3 осуществляют сдвиг в трех измерениях, т. е.
| [x y z 1] * |  |
=[x+yd+hz, bx+y+iz, cx+fy+z, 1]. |
4.Трехмерное вращение
Двухмерный поворот, рассмотренный ранее, является в то же время трехмерным поворотом вокруг оси Z . В трехмерном пространстве поворот вокруг оси Z описывается матрицей
Rz( )= )= |
 |
Матрица поворота вокруг оси X имеет вид
Rx( )= )= |
 |
Матрица поворота вокруг оси Y имеет вид
Ry( )= )= |
 |
Результатом произвольной последовательности поворотов вокруг осей x, y, z является матрица
| A= |  |
Подматрицу 3´3 называют ортогональной, так как ее столбцы являются взаимно ортогональными единичными векторами.
Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и сдвига нет.
Назад | Оглавление | Домой | Далее
Реферат на тему:
Матрица поворота
План:
- Введение
- 1Матрица поворота в двумерном пространстве
- 2Матрица поворота в трёхмерном пространстве
- 3Свойства матрицы поворота
Литература
Введение
|
|
Эта статья или раздел нуждается в переработке.
Пожалуйста, улучшите статью в соответствии с правилами написания статей. |
Матрицей поворота (или матрицей направляющих косинусов) называется матрица, умножение любого вектора на которую не меняет его длины.
1.
Матрица вращения
Матрица поворота в двумерном пространстве
В двумерном пространстве поворот можно описать одним углом θ со следующей матрицей линейного преобразования в декартовой системе координат:
Положительным углам при этом соответствует вращение против часовой стрелки в обычной, правосторонней системе координат, и по часовой в левосторонней системе координат.
Сам поворот происходит путём умножения матрицы поворота на вектор, описывающий вращаемую точку:
 .
.
2. Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой правой системы координат на угол α в трёхмерном пространстве являются:
 ,
,
 ,
,
 ,
,
В трёхмерном пространстве для описания поворота можно использовать
- три угла, например, углы Эйлера (γ,β,α),
- угол поворота θ и единичный вектор оси вращения
 ,
, - матрицу поворота 3×3,
- кватернион.
Матрицы поворота вектора в декартовой системе координат, соответствующие первым двум способам задания поворота:
и
Однако, поскольку умножение матриц не коммутативно, то есть: , следовательно, положение системы координат после поворота вокруг трех осей будет зависеть от последовательности поворотов, то существует 6 различных видов матрицы поворота:
- 1) Поворот около осей: X -> Y -> Z
- 2) Соответственно: X -> Z -> Y
- 3) Y -> X -> Z
- 4) Y -> Z -> X
- 5) Z -> X -> Y
- 6) Z -> Y -> X
Получить же нужную матрицу можно путем последовательного перемножения матриц поворота около одной оси (приведенных выше) в соответствии с желаемым порядком.
3. Свойства матрицы поворота
Если — матрица, задающая поворот вокруг оси
на угол φ, то:
Литература
- Лурье А. И. Аналитическая механика — М.:Физматлит — 1961 г. — 824 с.

8.1.1. Преобразование координат в трехмерном пространстве.
B основе программ аффинных преобразований пространственных объектов, а также их проецирования на картинную плоскость лежит аппарат однородных координат (см., например, СПИСОК ЛИТЕРАТУРЫ). При этом все необходимые для построения проекции и установления нужного ракурса преобразования координат описываются матрицами размером 4 ´ 4 и представляются в виде суперпозиции некоторых основных преобразований: переноса точки в пространстве на фиксированный вектор, поворота вокруг указанной оси на заданный угол, масштабирования вдоль какой-либо оси, сдвига, перспективы и проецирования на одну из главных координатных плоскостей.
Рис.8.1. Декартова система координат, проекция P’ точки P на плоскость XZ, сетка, на которой задана поверхность, и сечения, параллельные плоскостям XZ и YZ.
Основные преобразования координат. Pассмотрим некоторую декартову систему координат (рис.8.1). Любая точка пространства представляется в ней вектор-матрицей вида (х у z). Mы будем пользоваться однородными координатами точки в пространстве (х у z 1).
B качестве картинной плоскости выберем плоскость XZ, описываемую уравнением Y = 0. Проекция точки объекта на эту плоскость получается в результате умножения (х у z 1) ×A, где
задает преобразование проецирования на плоскость XZ.
Поворот вокруг заданной оси (X, Y и Z соответственно) на указанный угол a описываются следующими матрицами:
где а = sin a, b = соs a. Положительным считается поворот в направлении против часовой стрелки, если смотреть с конца оси, вокруг которой поворачивается объект.
Mатрицы преобразований переноса на фиксированный вектор и масштабирования имеют следующий вид:
Здесь (tx, ty, tz) – вектор переноса; sx, sy, sz — масштабные множители вдоль осей X, Y и Z соответственно, 1/s – множитель общего масштабирования.
Сдвиг заключается в том, что одна из координат точки (зависимая координата) изменяется на величину, пропорциональную одной из двух оставшихся координат (сдвигающей координате). Пусть зависимой координатой будет координата X, а сдвигающей – координата Y, тогда матрица сдвига будет иметь вид:
где F – коэффициент сдвига. Проекцию точек объекта на плоскость XZ из центра проекции C можно получить с помощью преобразования центрального проецирования. Eго матрица:
Здесь центр проекции лежит на оси Y и имеет Y-координату, равную (-H), где H > 0 (см. рис.8.1).
C помощью основных преобразований координат можно получить практически произвольные плоские геометрические проекции.
Pассмотрим сначала случай параллельного проецирования. В зависимости от того, какой угол образует направление проецирования с картинной плоскостью, параллельные проекции делятся на прямоугольные (например, аксонометрические проекции) и косоугольные. B случае прямоугольных проекций направление проецирования перпендикулярно картинной плоскости. В случае косоугольных проекций направление проецирования образует с картинной плоскостью угол, отличный от прямого. Более подробные сведения об этих типах проекций можно найти, например, в СПИСОК ЛИТЕРАТУРЫ.
Более общие аксонометрические проекции можно получить с помощью двух последовательных поворотов объекта (сначала вокруг оси Z на некоторый угол Az, а потом вокруг оси X на угол Aх) и затем ортогонального проецирования на плоскость XZ. Для двух наиболее распространенных типов аксонометрических проекций — изометрии и диметрии — углы поворота имеют следующие значения: Az = -45°, Aх = 35° и Az = -20°, Aх = 20°.
Hа рис.8.2 приведены примеры изометрической и диметрической проекций одной и той же поверхности, показано также как при этом проецируются на картинную плоскость оси декартовой системы координат.
Для построения косоугольных проекций удобно воспользоваться преобразованием сдвига. Одну из косоугольных проекций, например, можно построить следующей последовательностью преобразований:
1. сдвиг, в котором зависимой осью является ось X, сдвигающей осью — ось Y; коэффициент сдвига F = 1 в случае, если задана «положительная» проекция (рис.8.3, б), и F = -1, если требуется «отрицательная» проекция (рис.8.3, а);
2. сдвиг, в котором зависимой является ось Z, сдвигающей — ось Y и коэффициент сдвига F = 1;
3. проецирование на плоскость XZ.
B случае если ни одна из упомянутых стандартных параллельных проекций (изометрия, диметрия и косоугольная проекция) по каким-либо причинам не устраивает, можно построить требуемую проекцию с помощью переноса, поворота, масштабирования и сдвига.
Используя эти преобразования, можно также расположить нужным образом изображаемый объект в пространстве и затем построить какую-либо стандартную проекцию.
Рис.8.2. Диметрическая и изометрическая проекции поверхности, а также осей декартовой системы координат.
C помощью основных преобразований координат легко также формируется преобразование, которое позволит получать центральную проекцию объекта из произвольного центра проекции на плоскость, проходящую через начало координат перпендикулярно лучу зрения. Параллельная проекция тоже может быть задана по-другому — вектором направления проецирования, начало которого лежит в точке (0,0,0), а конец определяется программистом.
Tаким образом, для построения произвольной проекции графического объекта достаточно сформировать матрицу преобразования, являющегося суперпозицией перечисленных выше основных преобразований координат. Умножая матрицу координат произвольной точки справа на матрицу результирующего преобразования, получим координаты проекции этой точки на картинную плоскость в соответствии с выбранным способом проецирования.
Рис.8.3. «Отрицательная» (а) и «положительная» (б) косоугольные проекции поверхности, а также осей осей декартовой системы координат.
Далее описаны программы, реализующие основные преобразования координат, некоторые стандартные типы проекций, а также другие средства, необходимые для построения произвольных плоских геометрических проекций объектов.
Программы преобразований. Чтобы построить желаемую проекцию трехмерного объекта, нужно задать соответствующее преобразование.
Программы, определяющие преобразования, являются по сути установочными. Последовательность обращений к ним задает результирующее преобразование, соответствующее некоторому способу проецирования. Программы рисования будут использовать подготовленную матрицу преобразования для изображения объектов в выбранной проекции.
Kаждая из программ, устанавливающих свое преобразование, формирует матрицу размером 4 ´ 4 и умножает ее слева на матрицу текущего преобразования. B результате преобразования будут выполняться в том порядке, в котором они задавались. Hачальные установки выполняет программа INIT, которая формирует единичную матрицу. Обращение к ней отменяет уже накопленное преобразование. Очевидно, когда требуется получить новое результирующее преобразование, необходимо начинать с обращения к этой программе.
Получать некоторые стандартные проекции графических объектов позволяют программы ISOMET, DIMET, CABIN, VIEW, AXONOM. Однако иногда необходимо предварительно преобразовать объект (расположить некоторым образом в пространстве). Для этой цели можно воспользоваться программами, задающими поворот, растяжение, перенос, сдвиг. Это программы: TDROT, TDSCAL, TDTRAN, SHEAR.
Любое текущее преобразование можно сохранить (программа SAVETR) и при желании восстановить (программа SETTR). Bообще с помощью программы SETTR можно установить в качестве текущего преобразования произвольное преобразование, расширив тем самым круг основных преобразований координат.
Программа INIT производит инициализацию результирующего преобразования. Программа без параметров.
Программа TDTRAN(DX, DY, DZ) задает перенос объекта в пространстве относительно начала координат. Параметры программы DX,DY, DZ определяют вектор переноса.
Программа TDROT(NAXES,ALPHA) задает поворот системы координат относительно указанной оси на заданный угол. Eе параметры:
- NAXES
- номер оси, относительно которой выполняется поворот:
Значение Смысл 1 ось X, 2 ось Y, 3 ось Z. - Кроме того, если NAXES < 0, угол поворота считается заданным в радианах,
- NAXES > 0 — в градусах;
- ALPHA
- угол поворота:
- ALPHA > 0 — поворот выполняется против часовой стрелки, относительно оси, вокруг которой выполняется поворот;
- ALPHA < 0 — поворот выполняется по часовой стрелке.
Программа TDSCAL(NAXES,SCALE) позволяет выполнить растяжение (сжатие) вдоль указанной оси и, возможно, симметричное отражение объекта. Параметры программы следующие:
- NAXES
- номер оси, вдоль которой выполняется растяжение (сжатие):
Значение Смысл 1 ось X, 2 ось Y, 3 ось Z, 4 растяжение (сжатие) по всем осям; - SCALE
- коэффициент растяжения (сжатия):
- SCALE ³ 1 — растяжение в SCALE раз,
- SCALE О (0,1) — сжатие в 1/SCALE раз,
- SCALE < 0 симметричное отражение относительно соответствующей координатной плоскости или начала координат и растяжение в |SCALE| раз или сжатие в 1/|SCALE| раз.
Программа SHEAR(I,J,F) определяет сдвиг. Параметры программы:
- I
- номер сдвигающей координаты:
Значение Смысл 1 координата X, 2 координата Y, 3 координата Z; - J
- номер зависимой координаты;
- F
- коэффициент сдвига.
При I = J данное преобразование вырождается в преобразование масштабирования вдоль I-ой оси с коэффициентом растяжения равным (F+1).
Программа ISOMET формирует матрицу результирующего преобразования для получения изометрической проекции с учетом текущего преобразования.
6.Перенос и повороты в трехмерном пространстве.
Программа без параметров.
Программа DIMET позволяет сформировать матрицу результирующего преобразования для получения диметрической проекции с учетом текущего преобразования. Программа без параметров.
Программа CABIN(J) позволяет сформировать матрицу результирующего преобразования для получения косоугольной проекции с учетом текущего преобразования. Параметр программы J определяет вид косоугольной проекции. При J = 1 получается положительная проекция, а при J = -1 — отрицательная проекция.
Программа VIEW(X,Y,Z) позволяет сформировать матрицу центрального проецирования на плоскость, перпендикулярную лучу зрения. Параметры программы:
- X,Y,Z
- координаты центра проекции (точки зрения).
Изменяя координаты точки зрения можно получать различные проекции объекта. Для получения нужного ракурса иногда бывает удобнее перемещать в пространстве сам объект, оставляя центр проекции неподвижным. Этого можно достичь обращением к программам TDROT и TDTRAN (до вызова программы VIEW).
При обращении к программе VIEW надо следить, чтобы центр проекции не оказался внутри изображаемого объекта, иначе результаты работы программы рисования THREED будут непредсказуемы.
Программа AXONOM(X,Y,Z) формирует матрицу результирующего преобразования для получения аксонометрической проекции с учетом текущего преобразования. Hаправление проецирования определяется вектором, соединяющим точку (X,Y,Z) с началом координат.
Программа SAVETR(A) позволяет сохранить матрицу текущего преобразования в заданном массиве. Параметр программы:
- A
- одномерный массив длины 16.
Программа SETTR(A) позволяет занести в матрицу текущего преобразования содержимое заданного массива A. Предполагается, что в массиве A последовательно записаны столбцы матрицы размером 4 ´ 4.
Bспомогательные и служебные программы.
Программа HCUNIT(A) формирует единичную матрицу A размером 4 ´ 4.
Программа HCMULT(A,B) перемножает две квадратные матрицы четвертого порядка A ´B. Pезультат помещается на место матрицы A.
Программа HCPRSP(H) реализует преобразование центрального проецирования. Параметр H задает Y-координату центра проекции, расположенного на оси Y (H > 0).
Программа HCINV(X,Y,Z,XP,YP,ZP) вычисляет координаты (XP,YP,ZP) центра проекции с учетом обратного преобразования координат. Предварительно вычисляется матрица обратного преобразования.
Программа HCROT1(X,Y,Z) позволяет найти результирующее преобразование, переводящее двумя последовательными поворотами точку A(X,Y,Z) в точку с координатами ![]() .
.

FILED UNDER : IT


