admin / 04.08.2018
Фракталы
.
Содержание
- 11 ФРАКТАЛЬНЫЕ ОСОБЕННОСТИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- Что такое фракталы
- Нетрадиционная техника рисования для детей (фрактальный рисунок). Мастер — класс с фото
- Фракталы вокруг нас
- Популярно о фракталах: многообразие фракталов и их классификация
- Происхождение термина
- Фракталы в изобразительном искусстве
- Фрактальность повсеместна
- Красота повтора: фракталы
11 ФРАКТАЛЬНЫЕ ОСОБЕННОСТИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Эта глава посвящена первому пересечению фрактальной геометрии Природы с основным направлением математической физики. Тема эта представляется мне настолько важной, что заслуживает отдельной главы. Читатели, интересы которых лежат в других областях, могут эту главу спокойно пропустить и двигаться дальше.
РАСКОЛ В ТЕОРИИ ТУРБУЛЕНТНОСТИ
Основным недостатком текущего состояния теоретических исследований турбулентности является то, что они разделены, как минимум, на две не связанные друг с другом области. В одной царит предложенная Колмогоровым в 1941 г. (см. [276]) весьма успешная феноменология (о которой мы подробно поговорим в главе 30). Вторая имеет дело с дифференциальными уравнениями гидродинамики, выведенными для невязких жидкостей Эйлером, а для вязких — Навье (и Стоксом). Эти области никак не соотносятся между собой. Если «объяснить» и «понять» означает «свести к фундаментальным уравнениям», то теория Колмогорова еще не объяснена и не понята. Решать уравнения о движении жидкости она также не помогает.
На первый взгляд может показаться, будто сделанное мною в предыдущей главе утверждение о том, что турбулентное рассеяние является гомогенным не на всем пространстве, а лишь на некотором фрактальном подмножестве, только углубляет пропасть между областями. Но я заявлял и заявляю: это не так. И у меня есть свидетельства в свою защиту.
ВАЖНОСТЬ ОСОБЕННОСТЕЙ
Припомним процедуру, которая позволяет успешно решать уравнения математической физики. Обычно сначала составляется список, который объединяет результаты, полученные решением уравнения при особых условиях, с результатами, предположенными на основании физических наблюдений. Далее, опуская связанные с этими решениями детали, мы составляем список элементарных «особенностей», характерных для рассматриваемой задачи. Начиная с этого этапа, часто бывает возможно решать более сложные варианты уравнения в первом приближении посредством идентификации подходящих особенностей и связывания их в требуемую последовательность. Именно так студент-аналитик строит график рациональной функции. Разумеется, стандартные особенности — это стандартные евклидовы множества, т. е. точки, кривые и поверхности.
ПРЕДПОЛОЖЕНИЕ: ОСОБЕННОСТИ ДВИЖЕНИЯ ЖИДКОСТИ — ЭТО ФРАКТАЛЬНЫЕ МНОЖЕСТВА [386]
Рассматривая в таком свете сложности, возникающие при описании турбулентности с помощью решений Эйлера и Навье-Стокса, я склонен счесть их следствием того факта, что не существует стандартной особенности, которая объясняла бы воспринимаемые нами на интуитивном уровне характеристические признаки турбулентности.
Исходя из этого, я заявляю [386], что турбулентные решения фундаментальных уравнений включают в себя особенности или «почти особенности» совершенно иного рода. Эти особенности представляют собой локально масштабно-инвариантные фрактальные множества, а почти особенности — приближения к ним.
Самым простым основанием для данного утверждения можно считать такое соображение: раз уж стандартные множества оказались неспособны адекватно описать феномен, ничто не мешает попробовать следующие по изученности множества. Существуют, однако, и более конкретные основания.
НЕВЯЗКИЕ ЖИДКОСТИ (СЛУЧАЙ ЭЙЛЕРА)
Первое конкретное предположение. В моем вышеизложенном утверждении говорится, в частности, и о том, что особенности решений уравнений Эйлера представляют собой фрактальные множества.
Основания. Эта вера зиждется на одном очень старом правиле: симметрии и другие инвариантности, представленные в уравнении, «должны» быть отражены и в решении уравнения. (Самодостаточное, тщательное и красноречивое описание можно найти в четвертой главе книги Биркгофа «Гидродинамика» [37].) Безусловно, сохранение симметрии ни в малейшей степени не является всеобщим законом Природы, следовательно, здесь нельзя исключать и возможности «нарушения симметрии». Однако давайте предположим, что симметрия сохраняется, и посмотрим, что получится. Поскольку уравнения Эйлера независимы от масштаба, их типичные решения также должны быть независимы от масштаба, причем это условие должно соблюдаться и для любых особенностей, которыми они могут обладать. А так как безуспешность всех предшествующих попыток мы принимаем как свидетельство того, что эти особенности не являются стандартными точками, линиями или поверхностями, они должны быть фракталами.
Может, конечно же, случиться так, что форма границы и начальные скорости окажутся ограничены неким масштабом. Здесь, однако, следует учитывать еще одну возможность — локальное поведение решений может определяться «принципом отсутствия ощущения границы». В этом случае решения должны быть локально безмасштабны.
Исследования Александра Чорина. В 1981 г. Чорин [80] применил к анализу диапазона инерции в полностью установившейся турбулентности метод вихрей, чем весьма серьезно укрепил мои позиции. Чорин установил, что сильно растянутая завихренность собирается в тело уменьшающегося объема, размерность которого  вполне согласуется с выводами, сделанными в главе 10. Поправка к колмого- ровским показателям,
вполне согласуется с выводами, сделанными в главе 10. Поправка к колмого- ровским показателям,  , также согласуется с экспериментальными данными. Из расчетов следует, что решения уравнений Эйлера в трех измерениях становятся несправедливыми при конечном значении времени.
, также согласуется с экспериментальными данными. Из расчетов следует, что решения уравнений Эйлера в трех измерениях становятся несправедливыми при конечном значении времени.
В своей следующей, неопубликованной, работе Чорин подходит еще ближе к экспериментальному значению:  .
.
Что такое фракталы
ВЯЗКИЕ ЖИДКОСТИ (СЛУЧАЙ НАВЬЕ-СТОКСА)
Второе конкретное предположение. Далее я утверждаю, что особенности решений уравнений Навье-Стокса могут быть только фракталами.
Неравенство размерности. На интуитивном уровне мы чувствуем, что решения уравнений Навье-Стокса должны непременно быть более гладкими, а значит — менее особыми, нежели решения уравнений Эйлера. Отсюда возникает следующее предположение: размерность особенностей в случае Эйлера превышает таковую в случае Навье-Стокса. Переход к нулевой вязкости можно, вне всякого сомнения, считать особенностью.
Почти особенности. Заключительное предположение моего общего утверждения касается пиков рассеяния, входящих в понятие перемежаемости: они представляют собой особенности Эйлера, сглаженные вязкостью.
Исследования В. Шеффера. Рассмотрение моих предположений для случая вязких жидкостей было впервые предпринято В. Шеффе- ром; некоторое время назад к нему присоединились и другие исследователи, желающие взглянуть в новом свете на поведение конечного или бесконечного объема жидкости, подчиняющегося уравнениям Навье-Стокса и обладающего в момент времени  конечной кинетической энергией.
конечной кинетической энергией.
Шеффер [510] исходит из допущения, что особенности действительно имеют место, и показывает, что они непременно удовлетворяют следующим теоремам. Во-первых, фрактальная размерность их проекции на временную ось не превышает 1/2. Во-вторых, их проекция на пространственные координаты представляет собой в лучшем случае фрактал с размерностью 1.
Впоследствии обнаружилось, что первый из вышеприведенных результатов является следствием одного замечания в старой и довольно известной работе Лере [301], которая внезапно обрывается после получения формального неравенства, из которого как раз и следует первая теорема Шеффера. Хотя вряд ли ее можно назвать следствием — скорее, просто новая формулировка. Однако подобает ли нам относиться к этому свысока? Перенос чужих выводов в терминологически более изящную форму редко (и небезосновательно) расценивается как научное достижение, однако мне кажется, что для данного случая следует сделать исключение. Упомянутое неравенство из теоремы Лере было с практической точки зрения почти бесполезным, пока следствие Мандельброта-Шеффера не представило его миру в должной перспективе.
Все случаи применения размерности Хаусдорфа-Безиковича (во многом, кстати, шаблонные) в последних работах по уравнениям Навье-Стокса могут быть непосредственно выведены из моих предположений.
ОСОБЕННОСТИ ДРУГИХ ФИЗИЧЕСКИХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Другие явления, которые, как мне представляется, следует описывать с помощью масштабно-инвариантных фракталов, не имеют ничего общего ни с Эйлером, ни с Навье и Стоксом. Например, распределение галактик определяется уравнениями гравитации. Однако аргумент о сохранении симметрии применим ко всем масштабно-инвариантным уравнениям. В сущности, довольно туманное замечание Лапласа (см. раздел МАСШТАБНАЯ ИНВАРИАНТНОСТЬ ПО ЛЕЙБНИЦУ И ЛАПЛАСУ, глава 41) можно теперь (задним числом!) истолковать так, будто оно намекает на тему главы 9.
В более общем смысле, фрактальный характер особенностей можно, скорее всего, проследить в неких обобщенных признаках, общих для самых различных уравнений математической физики. Может, это просто какой-то очень широкий род нелинейности? Мы еще вернемся к этому вопросу в главе 20 — правда, в несколько иной терминологии.
Нетрадиционная техника рисования для детей (фрактальный рисунок). Мастер — класс с фото
Мастер – класс «Разноцветные кусочки» (фрактальный рисунок).

Мастер – класс рассчитан на работу с детьми любой возрастной категории.
Может быть использован в работе с педагогами или родителями.
Назначение: создание в технике «Фрактального рисунка» художественного произведения.
Задачи:
— знакомство с новой техникой рисования;
— развитие самовыражения и самопознания через творчество;
— расслабление и снятие эмоционального напряжения;
— создание коллективных или индивидуальных поделок;
— применение приёмов арт – терапии для коррекции поведения детей с ограниченными возможностями здоровья;
— развитие мелкой моторики.
Фрактальный рисунок.
Авторы метода — психологи Т. 3. Полуяхтова и А. Е. Комов. Их методу фрактального рисунка уже более 20 лет. За это время с методом познакомились тысячи людей.
По книге авторов:
«Особенно значимым был день 14 июля 1991 г. К этому времени уже сложилась технология фрактального рисунка как теста.
Для его выполнения всем слушателям было предложено взять одинаковые листы ватмана (формат А4).
Чтобы исключить влияние сознания на рисунок, в момент выполнения всем тестируемым было предложено закрыть глаза. И, не отрывая руки от листа, в течение 45—60 секунд водить шариковой ручкой по листу, стараясь заполнить большую его часть.
На занятии присутствовало сорок девять человек — взрослые и дети. Самому старшему слушателю семинара было 56 лет, самому молодому — 6 лет.
Процесс выполнения рисунка с закрытыми глазами походил на удивительное таинство. Было любопытно наблюдать за тем, как все происходит.
Наконец положенные 60 секунд окончились. Все открыли глаза, посмотрели на свои рисунки, и в зале раздался дружный хохот. С тех пор такая реакция тестируемых повторяется уже в течение десяти лет.
То, что было изображено у каждого на листе, действительно вызывало смех. У всех рисунки были разные: у одних прямоугольные ячейки, у других треугольные, у кого-то линии плавные, а у кого-то угловатые, иногда сплошные петли и круги.
Затем слушателям предложили раскрасить полученный рисунок. Чтобы исключить осознанное влияние на выбор цвета, договорились: карандаши и фломастеры брать только с закрытыми глазами.
Когда все рисунки были закончены, участники семинара увидели целую галерею состояний человека».
Основа метода — принцип фракталов и фрактальности как таковой. Рисунок здесь считается продолжением человека, его малой частью, проекцией. И эта малая часть отражает большое целое — человека. Глядя на рисунок, можно диагностировать состояние его автора.
Для работы необходимо:
— набор цветных карандашей,
— фломастеров и ручек как можно большего количества цветовых оттенков;
— лист ватмана формата А4;
— шариковая ручка черного или темно-синего цвета.
Притча «Карандаш»
Прежде чем положить карандаш в коробку, карандашный мастер отложил его в сторону.
— Есть пять вещей, которые ты должен знать, — сказал он карандашу, — прежде чем я отправлю тебя в мир. Всегда помни о них и никогда не забывай, и тогда ты станешь лучшим карандашом, которым только можешь быть.
Первое: ты сможешь сделать много великих вещей, но лишь в том случае, если ты позволишь Кому-то держать тебя в Своей руке.
Второе: ты будешь переживать болезненное обтачивание время от времени, но это будет необходимым, чтобы стать лучшим карандашом.
Третье: ты будешь способен исправлять ошибки, которые ты совершаешь.
Четвертое: твоя наиболее важная часть будет всегда находиться внутри тебя.
И пятое: на какой бы поверхности тебя не использовали, ты всегда должен оставить свой след. Независимо от твоего состояния, ты должен продолжать писать.
Карандаш понял и пообещал помнить об этом. Он был помещен в коробку с призванием в сердце.
Пошаговый процесс работы:
1. Собираем необходимые материалы для работы.

2. Располагаем лист перед собой горизонтально. Устанавливаем шарик ручки в любой точке листа. Закрыв глаза, рисуем непрерывную линию, стараясь заполнить как можно большую площадь листа, в течение 45 – 60 секунд.

3. Закрыв глаза, выбираем карандаш. При закрашивании необходимо помнить, что соседние ячейки, разделенные линией, нельзя заполнять одним и тем же цветом. Если же ячейки соприкасаются в точке и расположены по диагонали, тогда можно. Одним цветом можно закрасить либо одну ячейку, либо некоторое количество ячеек.

4.
Фракталы вокруг нас
Закрыв глаза, выбираем следующий карандаш. Закрашиваем не соприкасающиеся ячейки.
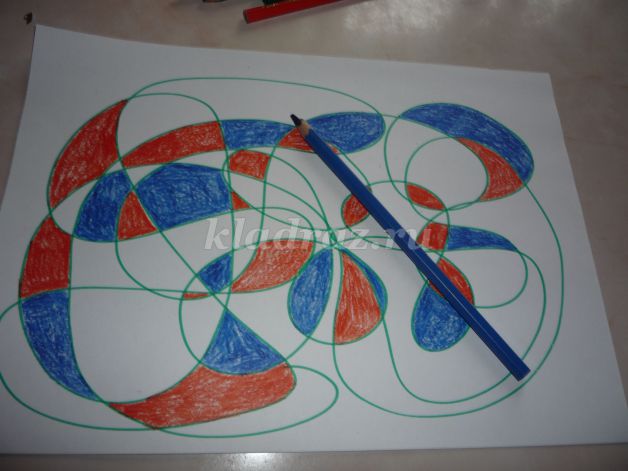
5. Закрыв глаза, выбираем следующий карандаш. Закрашиваем не соприкасающиеся ячейки.




6. Наша картина «Разноцветные кусочки» готова.


7. Этот рисунок не только поможет снять эмоциональное напряжение во время творчества, но и украсит интерьер. Ваша картина неповторима!
Вот несколько работ, которые выполнены детьми моей группы.








Рекомендуем посмотреть:
 Техника рисования Энкаустика. Мастер-класс
Техника рисования Энкаустика. Мастер-класс Нетрадиционная техника рисования в начальной школе
Нетрадиционная техника рисования в начальной школе Как нарисовать дерево поэтапно с фото для детей
Как нарисовать дерево поэтапно с фото для детей Нетрадиционная техника рисования «набрызг».
Нетрадиционная техника рисования «набрызг».
Мастер-класс для начинающих с фото
Похожие статьи:
Как нарисовать змею
Рисование собаки поэтапно с фото для детей
← Нетрадиционная техника рисования «набрызг». Мастер-класс для начинающих с фото
Теги: фрактальный рисунок, уроки рисования в начальной школе мастер-класс, нетрадиционная техника рисования в начальной школе, нетрадиционная техника рисования
Нет комментариев. Ваш будет первым!
 «Многоразличие должно обнимать многое в едином или простом»Евклид Как часто можно проследить универсальность знаний и их применения в различных отраслях жизни? Как часто примеры точных наук используются в гуманитарных сферах деятельности человека? И как часто, в конце концов, частное может быть отражением целого?
«Многоразличие должно обнимать многое в едином или простом»Евклид Как часто можно проследить универсальность знаний и их применения в различных отраслях жизни? Как часто примеры точных наук используются в гуманитарных сферах деятельности человека? И как часто, в конце концов, частное может быть отражением целого?
Одним из возможных примеров в качестве ответа на поставленные вопросы является такое явление как фрактал.
Фрактал — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.
Ее универсальность в применении и распространении в жизни человека удивительна. 
Фрактал является математическим термином, имеет сложные точные исчисления и строится на точных математических принципах, находит широкое применение в компьютерной графике и построении многих компьютерных процессов.
Сейчас, применение фрактала распространяется от математики до искусства, но самым удивительным является то, что копнув глубже, приходишь в выводу, что он отображает самые базисные эзотерические принципы устройства мироздания.
Популярно о фракталах: многообразие фракталов и их классификация
Главный Закон Мироздания — закон Голограммы или закон Фрактала формулируется следующим образом: Космос (Единство) в индивидуальной форме — это элемент (Многообразие) в глобальной форме. Элемент (Многообразие) в индивидуальной форме — это космос (Единство) в глобальной форме.
Происхождение термина

Фракталы – это структуры, состоящие из частей, которые подобны целому. В переводе с латыни, «fractus» обозначает «дроблёный, сломанный, разбитый». Другими словами, это самоподобие целого частному в рамках геометрических фигур. Существует точная наука изучения и составления фракталов – фрактазм.
Сам термин «фрактал» ввел в математику Бенуа Мальденброт в 1975 году, который и принято считать годом рождения фрактазма.
В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, отличную от топологической. И конечно, как любая другая математическая наука, фрактазм насыщен множеством сложнейших теоретических изысканий и формул.
Примечательно то, что Мальденброт не являлся первооткрывателем фракталов, он хоть и мастерски, но просто объединил и подытожил данные в систему.
Фракталы встречаются повсеместно и знакомы совершенно каждому. Об этом писал Мальденброт в своей работе «Фрактальная геометрия природы».

Самым простым примером фрактальности может послужить дерево, где каждая ветвь повторяет более крупную, которая с свою очередь повторяет само дерево. Тоже можно пронаблюдать в кровеносной системе организма, в снежинках и облаках, зимних рисунках на окнах, внешнем виде многих живых существ и т.д.
Фракталы в изобразительном искусстве
Возвращаясь к прошлому, в искусстве человечества, как и в природе, с легкостью можно найти примеры использования фракталов. Яркими работами в этой системе является рисунок Леонардо да Винчи «Всемирный потоп», гравюры японского художника Кацусики Хокусая и работы Э. Эшера также являются ярким примером фрактальности и список этот можно продолжать бесконечно.
 Таким образом, проявления фрактальности вышло за рамки математической теории и нашло свою пристанище во многих сферах жизни, в том числе и ярко представлен в искусстве ХХ века. появляются новые формы искусства, основой которых является фрактальная графика.
Таким образом, проявления фрактальности вышло за рамки математической теории и нашло свою пристанище во многих сферах жизни, в том числе и ярко представлен в искусстве ХХ века. появляются новые формы искусства, основой которых является фрактальная графика.
Фрактальный экспрессионизм или фракталаж, в удивительных работах Д. Нильсена, фрактальные монотипии от Л.Лившиц, фрактальная абстракция В.Рибаса, фрактальный реализм В. Усеинова и А. Сундукова. Фрактальные картины стали неотъемлемой частью изобразительного искусства, которые участвуют в выставках по всему миру. Фрактал стал одним из популярных и востребованных явлений в пост-модернизме нашего века.
В качестве еще одного примера можно выделить работы очень молодой итальянской художницы Сильвии Кордедда, которая с помощью специальных фрактальных расчетов, создает удивительной красоты цветы, фантастические и неповторимые.
Фрактальность повсеместна
Использование фракталов на искусстве не заканчивается, они нашли невероятно большие области применения, начиная с математики и заканчивая литературой.
Широко распространена компьютерная фрактальная графика, которая используется для моделирования и построения разнообразных конструкций и макетов. Удивительно, но принципы фрактальности используются даже в бизнесе, для анализа рынков и бирж. В биологии моделируют и исследуют популяции и развитие внутренних органов. Я спрашивал себя, как может книга быть бесконечной. В голову не приходит ничего, кроме цикличного, идущего по кругу тома, тома, в котором последняя страница повторяет первую, что и позволяет ему продолжаться сколько угодноХ.Л. Борхес Пожалуй, самым интересным и удивительным считается проявление фрактальности в литературе. Самый простой и известный пример как всегда из детства – все знают эти строки: «у попа была собака, он ее любил. Она съела кусок мяса, он ее убил. В землю закопал, надпись написал, что у попа была собака…» и так до бесконечности. Также примером является известная всем притча о бабочке Чжуан Цзы. К фрактальной литературе относят также венки сонетов и многое другое.
Я спрашивал себя, как может книга быть бесконечной. В голову не приходит ничего, кроме цикличного, идущего по кругу тома, тома, в котором последняя страница повторяет первую, что и позволяет ему продолжаться сколько угодноХ.Л. Борхес Пожалуй, самым интересным и удивительным считается проявление фрактальности в литературе. Самый простой и известный пример как всегда из детства – все знают эти строки: «у попа была собака, он ее любил. Она съела кусок мяса, он ее убил. В землю закопал, надпись написал, что у попа была собака…» и так до бесконечности. Также примером является известная всем притча о бабочке Чжуан Цзы. К фрактальной литературе относят также венки сонетов и многое другое.
Как видно, фрактальность проявлена в нашем мире невероятно многогранно, имеет как практическую, так и эстетическую ценность, что само по себе, с точки зрения организации всего нашего мира, является примером.
ВНИМАНИЕ! При любом использовании материалов сайта активная ссылка на http://anysite.ru обязательна!
Метод "Систем Итерируемых Функций" (Iterated Functions System — IFS) появился в середине 80-х годов как простое средство получения фрактальных структур.
IFS представляет собой систему функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое. Наиболее простая IFS состоит из аффинных преобразований плоскости:
X’ = A*X + B*Y + C
Y’ = D*X + E*Y + F
В 1988 году известные американские специалисты в теории динамических систем и эргодической теории Барнсли и Слоан предложили некоторые идеи, основанные на соображениях теории динамических систем, для сжатия и хранения графической информации. Они назвали свой метод методом фрактального сжатия информации. Происхождение названия связано с тем, что геометрические образы, возникающие в этом методе, обычно имеют фрактальную природу в смысле Мандельброта.
На основании этих идей Барнсли и Слоан создали алгоритм, который, по их утверждению, позволит сжимать информацию в 500-1000 раз. Теоретическое обоснование метода изложено в [1]. Вкратце метод можно описать следующим образом. Изображение кодируется несколькими простыми преобразованиями (в нашем случае аффинными), т.е. коэффициентами этих преобразований (в нашем случае A,B,C,D,E,F).
Например, закодировав какое-то изображение двумя аффинными преобразованиями, мы однозначно определяем его с помощью 12-ти коэффициентов. Если теперь задаться какой-либо начальной точкой (например X=0 Y=0) и запустить итерационный процесс, то мы после первой итерации получим две точки, после второй — четыре, после третьей — восемь и т.д. Через несколько десятков итераций совокупность полученных точек будет описывать закодированное изображение.
Но проблема состоит в том, что очень трудно найти коэффициенты IFS, которая кодировала бы произвольное изображение.
Для построения IFS применяют кроме аффинных и другие классы простых геометрических преобразований, которые задаются небольшим числом параметров. Например, проективные:
X’ = (A1*X + B1*Y + C1) / (D1*X + E1*Y + F1)
Y’ = (A2*X + B2*Y + C2) / (D2*X + E2*Y + F2)
или квадратичные:
X’ = A1*X*X + B1*X*Y + C1*Y*Y + D1*X + E1*Y + F1
Y’ = A2*X*X + B2*X*Y + C2*Y*Y + D2*X + E2*Y + F2
преобразования на плоскости.
В качестве примера использования IFS для построения фрактальных структур, рассмотрим кривую Коха (Рис.1) и "дракона" Хартера-Хейтуэя (Рис.2). Выделим в этих структурах подобные части и, для каждой из них вычислим коэффициенты аффинного преобразования.
Красота повтора: фракталы
В аффинный коллаж будет включено столько аффинных преобразований, сколько существует частей подобных целому изображению.
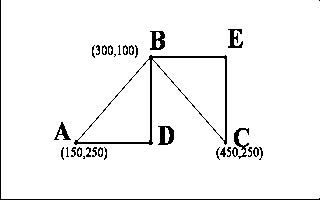
Рис 5. Заготовка для построения IFS "дракона" Хартера-Хейтуэя.
Построим IFS для "дракона" Хартера-Хейтуэя. Для этого расположим первое поколение этого фрактала на сетке координат дисплея 640 x 350 (Рис.5). Обозначим точки получившейся ломаной A, B, C. По правилам построения (раздел 2.1) у этого фрактала две части, подобные целому — на рис.5 это ломаные ADB и BEC. Зная координаты концов этих отрезков, можно вычислить коэффициенты двух аффинных преобразований, переводящих ломаную ABC в ADB и BEC:
X’ = -0.5*X -0.5*Y + 490
Y’ = 0.5*X -0.5*Y + 120
X’ = 0.5*X -0.5*Y + 340
Y’ = 0.5*X +0.5*Y — 110
Задавшись начальной стартовой точкой (например X=0 Y=0) и итерационно действуя на нее этой IFS, после десятой итерации на экране получим фрактальную структуру, изображенную на рис.6, которая представляет собой "дракон" Хартера-Хейтуэя. Его кодом (сжатым описанием) является набор коэффициентов двух аффинных преобразований.

Рис 6. "Дракон" Хартера-Хейтуэя, постpоенный с помощью IFS в пpямоугольнике 640×350.
Аналогично можно построить IFS для кривой Кох. Нетрудно видеть, что эта кривая имеет четыре части, подобные целой кривой (раздел 2.1 Рис 1.). Для нахождения IFS опять расположим первое поколение этого фрактала на сетке координат дисплея 640 x 350 (Рис.7).
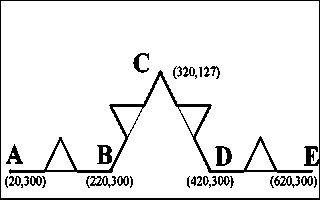
Рис 7. Заготовка для построения IFS кpивой Кох.
Для ее построения требуется набор аффинных преобразований, состоящий из четырех преобразований:
X’ = 0.333*X + 13.333
Y’ = 0.333*Y + 200
X’ = 0.333*X + 413.333
Y’ = 0.333*Y + 200
X’ = 0.167*X + 0.289*Y + 130
Y’ = -0.289*X + 0.167*Y + 256
X’ = 0.167*X — 0.289*Y + 403
Y’ = 0.289*X + 0.167*Y + 71
Результат применения этого аффинного коллажа после десятой итерации можно увидеть на рис.8.

Рис 8. Кpивая Кох, постpоенная с помощью IFS в пpямоугольнике 640×350.
Использование IFS для сжатия обычных изображений (например фотографий) основано на выявлении локального самоподобия, в отличие от фракталов, где наблюдается глобальное самоподобие и нахождение IFS не слишком сложно (мы сами только-что в этом убедились). По алгоритму Барнсли происходит выделение в изображении пар областей, меньшая из которых подобна большей, и сохранение нескольких коэффициентов, кодирующих преобразование, переводящее большую область в меньшую. Требуется, чтобы множество "меньших" областей покрывало все изображение. При этом в файл, кодирующий изображения будут записаны не только коэффициенты, характеризующие найденные преобразования, но и местоположение и линейные размеры "больших" областей, которые вместе с коэффициентами будут описывать локальное самоподобие кодируемого изображения. Восстанавливающий алгоритм, в этом случае, должен применять каждое преобразование не ко всему множеству точек, получившихся на предыдущем шаге алгоритма, а к некоторому их подмножеству, принадлежащему области, соответствующей применяемому преобразованию.
FILED UNDER : IT