admin / 30.06.2018
Параметрическая модель
Под параметрической моделью понимается математическая модель, позволяющая установить количественную связь между функциональными и вспомогательными параметрами системы.
Классификация моделей
2) Как определяется понятие моделирования?
Модели́рование — исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.
Виды мод-я:
В силу многозначности понятия «модель» в науке и технике не существует единой классификации видов моделирования: классификацию можно проводить по характеру моделей, по характеру моделируемых объектов, по сферам приложения моделирования (в технике, физических науках, кибернетике и т. д.). Например, можно выделить следующие виды моделирования:
- Информационное моделирование
· Компьютерное моделирование
· Математическое моделирование
· Математико-картографическое моделирование
· Цифровое моделирование
· Логическое моделирование
· Статистическое моделирование
· Структурное моделирование
· Физическое моделирование
· Экономико-математическое моделирование
· Имитационное моделирование
· Графическое и геометрическое моделирование
· Натурное моделирование и т. д.
Процесс моделирования включает три элемента:
· субъект (исследователь),
· объект исследования,
· модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.
Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.
На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.
На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.
Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.
Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.
3)Что наз.гипотезой и аналогией в исследования объекта?
В научных исследованиях большую роль играют гипотезы, т. е.определенные предсказания, основывающиеся на небольшом количестве опытных данных, наблюдений, догадок. Быстрая и полная проверка выдвигаемых гипотез может быть проведена в ходе специально поставленного эксперимента. При формулировании и проверке правильности гипотез большое значение в качестве метода суждения имеет аналогия.
Аналогией называют суждение о каком-либо частном сходстведвух объектов, причем такое сходство может быть существенным и несущественным.Необходимо отметить, что понятия существенности и несущественности сходства или различия объектов условны и относительны. Существенность сходства (различия) зависит от уровня абстрагирования и в общем случае определяется конечной целью проводимого исследования. Современная научная гипотеза создается, как правило, по аналогии с проверенными на практике научными положениями. Таким образом, аналогия связывает гипотезу с экспериментом.
Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам; такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Другими словами, модель (лат. modulus — мера) -это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.
4)Чем отличается использование метода моделирования, при внешнем и внутреннем проектировании?
Независимо от разбиения конкретной сложной системы на подсистемы при проектировании каждой из них необходимо выполнить внешнее проектирование (макропроектирование) и внутреннее проектирование (микропроектирование). Так как на этих стадиях разработчик преследует различные цели, то и используемые при этом методы и средства моделирования могут существенно отличаться. На стадии макропроектирования должна быть разработана обобщенная модель процесса функционирования сложной системы, позволяющая разработчику получить ответы на вопросы об эффективности различных стратегий управления объектом при его взаимодействии с внешней средой. Стадию внешнего проектирования можно разбить на анализ и синтез. При анализе изучают объект управления, строят модель воздействий внешней среды, определяют критерии оценки эффективности, имеющиеся ресурсы, необходимые ограничения. Конечная цель стадии анализа -построение модели объекта управления для оценки его характеристик. При синтезе на
этапе внешнего проектирования решаются задачи выбора стратегии управления на основе модели объекта моделирования, т. е. сложной системы.
На стадии микропроектирования разрабатывают модели с целью создания эффективных подсистем. Причем используемые методы и средства моделирования зависят от того, какие конкретно обеспечивающие подсистемы разрабатываются: информационные, математические, технические, программные и т. д.
5)Объясните понятие «моделирование объектов управления»
При изучении любых объектов (технических систем, процессов, явлений) основной задачей является построение их моделей. Как результат познания модель представляет собой отображение в той или иной форме свойств, закономерностей, физических и других характеристик, присущих исследуемому объекту. Характер модели определяется поставленными целями и может быть различным в зависимости от ее назначения. Модели разделяют на два основных класса: символические (словесные описания, схемы, чертежи, математические уравнения и т. д.) и вещественные (макеты, разного рода физические аналоги и электронные моделирующие устройства, имитирующие процессы в объектах)
При исследовании объектов, предназначенных для управления, применяют математические модели, входящие в класс символических, и вещественные. К математическим моделям относится такое математическое описание, которое адекватно отражает как статические, так и динамические связи между входными и выходными переменными объекта. Математическая модель может быть получена и аналитически (закономерности протекающих в объекте процессов полностью известны), и по результатам экспериментального исследования входных и выходных переменных объекта без изучения его физической сущности. Последний подход особенно широко используется на практике, так как позволяет обойтись минимумом априорных сведений об объекте при построении его модели.
Для управления объектом необходимо иметь модель в виде математического описания, устанавливающего связь между входными и выходными переменными в форме, на основе которой может быть выбран закон управления, обеспечивающий заданное функционирование объекта. Получаемое описание должно давать преобразования воздействия на объект u в реакцию объекта y. Переменные u и y могут представлять собой функции одинаковых и разных аргументов.
Преобразование одной функции в другую производится оператором, который определяет совокупность математических или логических операций, устанавливающих соответствие между ними: y(t)=A{u(t)}.
В качестве примера можно назвать операторы дифференцирования, интегрирования и т. п. Для стационарных линейных одномерных объектов оператор может быть задан в виде дифференциального уравнения или системы дифференциальных уравнений первого порядка, интегральной свертки, частотной характеристики (передаточной функции) объекта.
На практике объекты стремятся описывать линейными стационарными моделями, хотя в действительности все объекты в той или иной мере обладают свойствами нелинейности, нестационарности, распределенности, стохастичности.
Использование более простых операторов следует рассматривать как попытку аппроксимации характеристик сложного объекта упрощенным приближенным описанием, но удобным для дальнейших расчетов. Описания могут быть заданы различным образом: аналитически, таблично, в виде разложения по какой-либо системе функций и т. д.
⇐ Предыдущая12345678910Следующая ⇒
Дата публикования: 2015-01-26; Прочитано: 1213 | Нарушение авторского права страницы

Параметрическое моделирование (параметризация) — моделирование (проектирование) с использованием параметров элементов модели и соотношений между этими параметрами. Параметризация позволяет за короткое время «проиграть» (с помощью изменения параметров или геометрических соотношений) различные конструктивные схемы и избежать принципиальных ошибок.
Параметрическое моделирование существенно отличается от обычного двумерного черчения или трёхмерного моделирования. Конструктор в случае параметрического проектирования создаёт математическую модель объектов с параметрами, при изменении которых происходят изменения конфигурации детали, взаимные перемещения деталей в сборке и т. п.
Идеи параметрического моделирования появились ещё на ранних этапах развития САПР, но какое-то время не могли быть осуществлены по причине недостаточной компьютерной производительности.
Первые известные САПР с возможностью параметризации вышли в 1989 году. Первопроходцами были Pro/Engineer (трёхмерное твердотельное параметрическое моделирование) фирмы Parametric Technology Corporation и T-FLEX CAD (двумерное параметрическое моделирование) фирмы Топ Системы[1][2]
Содержание
- Двумерное параметрическое черчение и моделирование
- Трёхмерное твердотельное параметрическое моделирование
- Типы параметризации
- Параметрическая модель
- Примечания
- См. также
- Ссылки
- Геометрическое моделирование в САПР
- Важные термины параметрического моделирования в MicroStation
- Параметрическая модель стула
- Содержание
- Введение
- Параметрическое моделирование
- Описание модели стула
- MAXScript-реализация модели стула
- Запуск программы
- Описание программы
- Заключение
- Источники
Двумерное параметрическое черчение и моделирование
Параметризация двумерных чертежей обычно доступна в CAD-системах среднего и тяжёлого классов[неизвестный термин]. Однако ставка в этих системах сделана на трёхмерную технологию проектирования, и возможности параметризации двухмерных чертежей практически не используются. Параметрические CAD-системы, ориентированные на двухмерное черчение (лёгкий класс), зачастую являются «урезанными» версиями более продвинутых САПР.
Трёхмерное твердотельное параметрическое моделирование
Трёхмерное параметрическое моделирование является гораздо более эффективным (но и более сложным) инструментом, нежели двумерное параметрическое моделирование. В современных САПР среднего и тяжёлого классов наличие параметрической модели заложено в идеологию самих САПР. Существование параметрического описания объекта является базой для всего процесса проектирования.
Типы параметризации
Табличная параметризация
Табличная параметризация заключается в создании таблицы параметров типовых деталей. Создание нового экземпляра детали производится путём выбора из таблицы типоразмеров. Возможности табличной параметризации весьма ограничены, поскольку задание произвольных новых значений параметров и геометрических отношений обычно невозможно.
Однако табличная параметризация находит широкое применение во всех параметрических САПР, поскольку позволяет существенно упростить и ускорить создание библиотек стандартных и типовых деталей, а также их применение в процессе конструкторского проектирования.
Иерархическая параметризация
Иерархическая параметризация (параметризация на основе истории построений) заключается в том, что в ходе построения модели вся последовательность построения отображается в отдельном окне в виде «древа построения». В нем перечислены все существующие в модели вспомогательные элементы, эскизы и выполненные операции в порядке их создания.
Помимо «древа построения» модели, система запоминает не только порядок её формирования, но и иерархию её элементов (отношения между элементами). Пример: сборки → подсборки → детали.
Параметризация на основе истории построений присутствует во всех САПР, использующих трёхмерное твердотельное параметрическое моделирование. Обычно такой тип параметрического моделирования сочетается с вариационной и/или геометрической параметризацией.
Вариационная (размерная) параметризация
Вариационная, или размерная, параметризация основана на построении эскизов (с наложением на объекты эскиза различных параметрических связей) и наложении пользователем ограничений в виде системы уравнений, определяющих зависимости между параметрами.
Процесс создания параметрической модели с использованием вариационной параметризации выглядит так:
- На первом этапе создаётся эскиз (профиль) для трёхмерной операции. Далее на эскиз накладываются необходимые параметрические связи.
- Затем эскиз «образмеривается», уточняются отдельные размеры профиля. На этом этапе отдельные размеры можно обозначить как переменные (например, параметру, обозначающему длину некой детали, присвоить имя «Length») и задать зависимости других размеров от этих переменных в виде формул (например, «Radius=Length/2»)
- Затем производится трёхмерная операция (например, выдавливание), значение атрибутов операции тоже служит параметром (например, величина выдавливания).
- В случае необходимости создания сборки взаимное положение компонентов сборки задаётся путём указания сопряжений между ними (совпадение, параллельность или перпендикулярность граней и рёбер, расположение объектов на расстоянии или под углом друг к другу и т. п.).
Вариационная параметризация позволяет легко изменять форму эскиза или величину параметров операций, что позволяет удобно модифицировать трёхмерную модель.
Геометрическая параметризация
Геометрической параметризацией называется параметрическое моделирование, при котором геометрия каждого параметрического объекта пересчитывается в зависимости от положения родительских объектов, его параметров и переменных.
Параметрическая модель, в случае геометрической параметризации, состоит из элементов построения и элементов изображения.
Параметрическая модель
Элементы построения (конструкторские линии) задают параметрические связи. К элементам изображения относятся линии изображения (которыми обводятся конструкторские линии), а также элементы оформления (размеры, надписи, штриховки и т. п.).
Одни элементы построения могут зависеть от других элементов построения. Элементы построения могут содержать и параметры (например, радиус окружности или угол наклона прямой). При изменении одного из элементов модели все зависящие от него элементы перестраиваются в соответствии со своими параметрами и способами их задания.
Процесс создания параметрической модели методом геометрической параметризации выглядит так:
- На первом этапе конструктор задаёт геометрию профиля конструкторскими линиями и отмечает ключевые точки.
- Далее проставляет размеры между конструкторскими линиями. На этом этапе можно задать зависимость размеров друг от друга.
- Затем обводит конструкторские линии линиями изображения — получается профиль, с которым можно осуществлять различные трёхмерные операции.
Последующие этапы в целом аналогичны процессу моделирования методом вариационной параметризации.
Геометрическая параметризация позволяет более гибко редактировать модели. Если надо внести незапланированное изменение, то в геометрию модели не обязательно удалять исходные линии построения (это может привести к потере ассоциативных взаимосвязей между элементами модели), — можно провести новую линию построения и перенести на неё линию изображения.
Примечания
См. также
Ссылки
Геометрическое моделирование в САПР
Примерный перечень вопросов к государственному экзамену
По специальности САПР
(2012-2013уч.год)
Лингвистическое и программное
Обеспечение САПР
1.
Важные термины параметрического моделирования в MicroStation
Проблематика разработки ЛО САПР. Понятие входного языка САПР и языкового процессора. Обобщенная модель процесса компиляции. Способы реализации языковых процессоров САПР.
2. Языки программирования и формальные языки. Понятие транслятора и компилятора. Фазы компиляции. Инструменты и технологии разработки и реализации языков программирования.
3. Способы задания формальных языков (ФЯ). Задание ФЯ при помощи грамматик и распознавателей (привести примеры грамматик и
распознавателей ).
4. Соответствия между способами задания языков. Соответствия между КС-грамматиками и МП-автоматами. Построение МП-автомата, моделирующего левые выводы по заданной КС-грамматике (построить МП-автомат для конкретной КС-грамматики).
5. Понятие о переводе (трансляции). Модели трансляторов (конечные преобразователи и преобразователи с магазинной памятью).
6. Определение синтаксического разбора. Модели анализаторов. Построение левого анализатора по заданной КС-грамматике.
7. Общая характеристика процесса сканирования. Методика конструирования сканера (характеристика каждого этапа построения сканера и применяемые методы). Представление результатов сканирования.
8. Классы лево- и право- анализируемых грамматик (определения) . LL(k)- грамматики, их свойства и роль в разработке языков программирования. Приведение грамматик к LL-форме (устранение рекурсии и факторизация). Привести пример устранения левой рекурсии.
9. Общая модель процесса компиляции. Понятие синтаксического анализа. Общая характеристика моделей и методов детерминированного синтаксического анализа. Модель LL(k)- анализатора.
10. Основные функции семантического анализа. Способы представления промежуточной программы. Применение моделей синтаксически управляемой трансляции (СУ-перевода) в разработке анализаторов.
Разработка САПР
1. Интерфейс программы Autocad
2. Ядро Parasolid в T-Flex
3. Панели инструментов программы Autocad
4. Сравнение программ МКЭ
5. Анимация в Blender
6. Обзор возможностей пакета Abacus Student
7. Программирование в среде Visual LISP
8. Проект освещения NanoCAD-Электро
9. Основы метода конечных элементов
Интеллектуальные подсистемы в САПР
1. Формальные системы. Способ описания, основная терминология. Логики высказываний как формальная система. Прямая и обратная дедукция. Метод резолюций для логики высказываний.
2. Модель логики предикатов первого порядка. Основные понятия логики предикатов. Логика предикатов как формальная система.
3. Унификация в логике предикатов первого порядка. Приведение формул логики предикатов к множеству предложений. Метод резолюций для логики предикатов первого порядка.
4. Продукционные модели. Методы построения вывода в этих моделях. И/ИЛИ графы.
5. Семантические сети. Основные концепции, используемые в семантических сетях. Поиск решения в семантических сетях.
6. Фреймы и сценарии. Примеры фреймов и сценариев.
7. Нечеткие знания, виды нечеткостей. Нечеткость, связанная с недетерминированным выводом.
8. Нечеткие знания, виды нечеткостей. Нечеткости, связанные с недостоверностью знаний. Метод Байеса. Метод MYCIN.
9. Задача планирования. Планирование в пространстве состояний и планирование в пространстве задач. Алгоритмы и методы построения планов.
10. Экспертные системы (ЭС). Основные составляющие ЭС и их назначение. Статические и динамические ЭС. Этапы разработки ЭС и их сущность.
Геометрическое моделирование в САПР
1. Аффинные преобразования в пространственном и плоскостном случае геометрического моделирования. Основные типы и свойства аффинных преобразований. Композиция аффинных преобразований. Аффинные преобразования в локальной системе отсчета. Применение аффинных преобразований для деформаций геометрических моделей.
2. Основные принципы аппроксимации кривой сплайнами в геометрическом моделировании. Принципы построения составной кривой при помощи соединения («склейки») или суперпозиции частичных сплайнов.
3. Минимально-достаточная степень полинома для аппроксимации участка кривой (частичного сплайна) между двумя опорными точками в геометрическом моделировании. Требуемый порядок аппроксимирующей функции для обеспечения условий непрерывности и гладкости составной сплайн-кривой, кривизны и кручения участка кривой.
4. Составные сплайны Безье в геометрическом моделировании. Обеспечение условий непрерывности и гладкости. Уравнения «склейки» частичных сплайнов в векторной и параметрической форме для классического сплайна Безье. Характеристическая ломаная кривой Безье. Случаи получения кривых переменной вогнутости и самопересечения кривой
5. Базисные сплайны (В-сплайны) в геометрическом моделировании. Свойства частичного В-сплайна. Составные В-сплайны (NURBS). Принцип суперпозиции В-сплайнов при построении составных кривых. Случай использования нормированных В-сплайнов. Весовые коэффициенты.
6. Основные способы построения геометрических моделей пространственных объектов инструментальными средствами компьютерной графики. Полигональное представление поверхности на этапе визуализации в инструментальных комплексах.
7. Метод каркасного геометрического моделирования поверхностей пространственных объектов инструментальными средствами компьютерной графики.
8. Метод твердых тел геометрического моделирования пространственных объектов инструментальными средствами компьютерной графики.
9. Метод геометрического моделирования поверхностей пространственных объектов инструментальными средствами компьютерной графики при помощи плоских кривых (лофтинг). Метод геометрического моделирования поверхности вращения и метод выдавливания как частные случаи лофтинга.
10. Методы геометрического моделирования поверхностей пространственных объектов инструментальными средствами компьютерной графики при помощи сплайн-структур. Геометрическое моделирование поверхностей при помощи двухпараметрических сплайнов Безье (patch-моделирование). Геометрическое моделирование поверхностей при помощи пространственных (двухпараметрических) В-сплайнов (NURBS).
Объектно-ориентированное программирование
1. Перечислить и дать характеристику основным причинам сложности программного обеспечения. Общие признаки любой сложной системы; приемы борьбы со сложностью ПО.
2. Перечислить и дать характеристику основным разновидностям стилей (парадигм) программирования. Роль объектно-ориентированной парадигмы. Основные и дополнительные элементы объектной модели.
3. Ссылки в языке С++, использование ссылок. Отличие ссылок от указателей. Передача аргументов функций по ссылке. Перегрузка функций; правила перегрузки.
4. Общее понятие класса языка С++. Классы как абстрактные типы данных. Синтаксис описания класса. Виды членов класса. Управление доступом к членам класса. Инкапсуляция. Интерфейс и реализация класса. Объекты (экземпляры) класса и способы их создания.
5. Конструкторы и деструкторы класса. Виды конструкторов класса: конструктор по умолчанию, копирующий конструктор, конструкторы преобразования типа, прочие конструкторы. Правила вызова конструкторов различных видов. Вызов деструктора.
6. Перегрузка операций для классов. Назначение и способы перегрузки. Принципы и правила перегрузки операций. Пример перегрузки операции «=». Рекомендации по перегрузке операций; правильные форматы перегруженных операций.
7. Перечислить и дать характеристику видов отношений между классами. Привести примеры для каждого вида отношений.
8. Отношение между классами типа «наследование». Отличия наследования от агрегации. Иерархия наследования. Синтаксис наследования. Открытое и закрытое наследование. Назначение «защищенных» (protected) членов базового класса. Виртуальные функции и их назначение. Полиморфизм. Виртуальные деструкторы и правила их использования. Чисто виртуальные функции и абстрактные классы. Наследование интерфейса и наследование реализации.
9. Концепция параметризуемых типов (шаблонов) в языке С++. Шаблоны классов. Различия между шаблонами и классами. Синтаксис описания шаблона. Создание объекта шаблонного класса (инстанцирование шаблона). Шаблоны функций. Связь между шаблонами функций и перегрузкой.
10. Понятие исключения (особой ситуации). Механизм обработки исключений. Синтаксические конструкции языка для обработки исключений. Различение особых ситуаций. Имена особых ситуаций. Группирование исключений. Повторная генерация исключений; перехват всех исключений.
Структуры и алгоритмы обработки данных
1. Линейные списки – стеки, очереди, деки. Набор процедур для работы со связанным стеком, очередью.
2. Кольцевые списки. Многосвязные списки, примеры применения.
3. Древовидная структура, основные понятия. Способы обхода бинарного дерева.
4. Дерево поиска. Включение элементов. Удаление элементов из дерева поиска.
5. В-деревья, их свойства, построение. Индексирование массивов данных. Индексные деревья.
6. Применение бинарных деревьев. Кодирование и сжатие данных.
Кодовые деревья, дерево Хаффмена.
7. Сортировка. Методы вставок и обмена. Метод Шелла. Быстрая сортировка. Обменная поразрядная сортировка.
8. Сортировка. Методы выбора и слияния. Простой, квадратичный выбор. Выбор из дерева. Двухпутевое слияние. Метод слияния списков.
9. Алгоритмы поиска данных. Последовательный, двоичный, блочный, интерполяционный, Фибоначчиев поиск.
10. Хеширование, хеш-функции. Способы разрешения коллизий.
©2015-2018 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Нарушение авторских прав и Нарушение персональных данных
Список примеров
Параметрическая модель стула
Содержание
Введение
В параметрической модели имеется взаимосвязь параметров ее различных компонентов.
Параметрическое моделирование
В такой модели изменение значения одного параметра влечет изменения значений связанных с ним параметров модели. Подобные модели широко применяются в САПР. Примером такой модели в 3ds Max может служить объект Biped (двуногий).
3ds Max позволяет создавать параметрические модели посредством связывания параметров, употребления соответствующих контроллеров и модификаторов (преимущественно параметрических), а также за счет создания соответствующего MAXSript-кода, обеспечивающего пересчет модели при изменении значения управляющего параметра.
Рассмотрим параметрическую модель (рис. 1, а), в которой реализуются следующие зависимости:
R = abs(0.25 * H);
spherePosition = conePosition + [0, 0, 1.25 * H],
где
R – радиус сферы;
H – высота конуса;
spherePosition – позиция сферы (координаты ее центра);
conePosition – позиция конуса (координаты центра его основания).
 |
 |
| а | б |
|
Рис. 1. Параметризованная модель: а – H = 50; б – H = -50 |
Рассматриваемую модель можно реализовать в 3ds Max несколькими способами. Приведем два из них. В первом употребим контроллеры Float Expression и Position Expression для формирования соответственно первой и второй зависимостей, а во втором – контроллеры Float Script и Position Script.
Создание модели и ее параметризацию средствами контроллеров Float Expression и Position Expression обеспечит следующий код:
delete $*
h = 50
cn = cone radius1:20 radius2:0 height:70 heightSegs:20 sides:24 wireColor:[6, 135, 113]
sph = sphere radius:(0.25 * cn.Height) segs:32 wireColor: [135, 110, 8]
sph.Pos = cn.Pos + [0, 0, 1.25 * cn.Height]
cn.Height.Controller = bezier_float()
fltX = float_expression()
fltX.AddScalarTarget «h» cn.Height.Controller
fltX.SetExpression «abs(0.25 * h)»
sph.Radius.Controller = fltX
—
pstnX = position_expression()
pstnX.AddScalarTarget «h» cn.Height.Controller
pstnX.AddVectorTarget «ps» cn.Position.Controller
pstnX.SetExpression «ps + [0, 0, 1.25 * h]»
sph.Position.Controller = pstnX
animate on (
at time 0f (cn.Height = h; cn.Pos = [0, 0, 0])
at time 50f (cn.Height = -h; cn.Pos = [0, 0, h])
at time 100f (cn.Height = h; cn.Pos = [0, 0, 0])
)
playAnimation()
Порядок действий следующий:
- Сцена очищается, и создаются объекты конус и сфера с именами cn и sph соответственно.
- После создания контроллера fltX (применяется конструктор float_expression) в контроллере создается скалярная переменная h, зависящая от высоты конуса (метод AddScalarTarget): значение переменной h будет равняться высоте конуса. Предварительно этому параметру (высоте конуса) назначается контроллер Bezier Float, ссылка на который используется в качестве второго параметра метода AddScalarTarget.
- Далее задается выражение (метод SetExpression), результат которого возвращает контроллер fltX.
- Параметру сферы Radius назначается контроллер fltX.
Теперь изменение высоты конуса, например на вкладке Modify после выбора конуса, приведет к изменению радиуса сферы.
Для управления позицией сферы используется контроллер Position Expression, программируемый в следующем порядке:
- После создания контроллера pstnX (применяется конструктор position_expression) в контроллере создаются скалярная переменная h, зависящая от высоты конуса (метод AddScalarTarget), и векторная переменная ps, зависящая от позиции конуса (метод AddVectorTarget).
Как и в случае метода AddScalarTarget, вторым параметром метода AddVectorTarget также является ссылка на контроллер (cn.Position.Controller). Значение переменной ps после установления такой связи будет равно значению позиции конуса (величина типа Point3).
- Далее задается выражение (метод SetExpression), результат которого возвращает контроллер pstnX.
- Свойству сферы Position назначается контроллер pstnX.
Наличие такого контроллера обеспечит надлежащее перемещение сферы при изменении позиции конуса.
Для демонстрации результата в точках 0f, 50f и 100f временной шкалы создаются ключи анимации высоты и позиции конуса.
После запуска программы можно открыть диалог настройки контроллера, например Float Expression (рис. 2), выполнив следующие действия: выбрать примитив Sphere – меню Graph Editors – Track View – Curve Editor – ветвь Objects – Sphere01 – Sphere (Object) – Radius – двойной удар мышью.
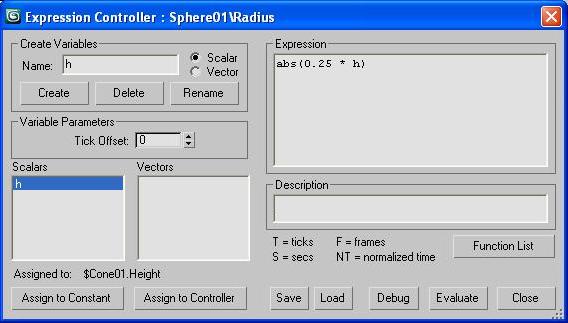
Рис. 2. Диалог настройки контроллера Float Expression
Порядок запуска MAXScript-кода в 3ds Max описан ниже.
Вторая реализация рассматриваемой модели, основанная на контроллерах Float Script и Position Script, поддерживается следующим кодом:
delete $*
h = 50
cn = cone radius1:20 radius2:0 height:70 heightSegs:20 sides:24 wireColor:clr
sph = sphere radius:(0.25 * cn.Height) segs:32 wireColor:clr2
sph.Pos = cn.Pos + [0, 0, 1.25 * cn.Height]
fltS = float_script()
fltS.AddNode «cn2» cn
fltS.Script = «abs(0.25 * cn2.Height)»
sph.Radius.Controller = fltS
—
psS = position_script()
psS.AddNode «cn2» cn
psS.Script = «cn2.Pos + [0, 0, 1.25 * cn2.Height]»
sph.Position.Controller = psS
animate on (
at time 0f (cn.Height = h; cn.Pos = [0, 0, 0])
at time 50f (cn.Height = -h; cn.Pos = [0, 0, h])
at time 100f (cn.Height = h; cn.Pos = [0, 0, 0])
)
playAnimation()
В обоих контроллерах определяется переменная cn2 (метод AddNode), хранящая ссылку на объект конус. Это обеспечивает доступ к свойствам конуса, что и используется соответствующим образом в Script-выражениях контроллеров (свойство Script).
С другими возможностями программного управления моделями 3ds Max можно познакомиться, обратившись, например, к источникам [1] и [2].
Рассмотренную модель можно, разумеется, реализовать интерактивно, без применения MAXScript. Следующая модель такой альтернативы не имеет.
Описание модели стула
В рассматриваемом примере регулируемым параметром является радиус скруглений R между отдельными компонентами модели стула. Изменение радиуса влечет изменение высоты ножек стула, размеров его сиденья и спинки (рис. 3).
 |
 |
| а | б |
|
Рис. 3. Параметризованный стул: а — R = 5; б — R = 15 |
Модель имеет следующие характеристики:
- Радиус всех скруглений одинаков и изменяется с шагом 1 в диапазоне 5 – 15 единиц.
- При пересчете модели сохраняются габариты стула, хранимые глобальными переменными wX, wY и wZ, а также размеры и положение задних ножек стула.
- Каркас стула воспроизводится цилиндрами и дугами (примитивы Cylinder и Arc); последние используются для отображения скруглений.
- Сиденье и списка стула отображаются посредством примитива Plane (плоскость).
- Сиденье отстоит от основания стула на 0.5 * wZ.
MAXScript-реализация модели стула
Параметризация модели выполняется средствами MAXScript. Код, обеспечивающий построение и управление моделью, а также создание и вывод управляющего диалога, имеет следующий вид:
global rlFlt
global clr = [6, 135, 113], clr2 = [135, 110, 8]
global wX = 60.0, wY = 45.0, wZ = 120.0
global arrC = #(), arrRc = #()
—
fn Prps = (
delete $*
units.DisplayType = #Generic
units.SystemType = #Inches
viewport.SetLayout #layout_4
viewport.ActiveViewport = 4
max vpt persp user
viewport.SetGridVisibility 4 false
max tool zoomExtents
backgroundColor = color 200 200 200
)
—
fn fndPs R wX wY wZ &arrPs = (
x = 0.5 * wX
y = 0.5 * wY
vY = [0, wY, 0]
wZ2 = 0.5 * wZ
p1 = [-x, -y, 0]; p2 = p1 + vY
p3 = [x, -y, 0]; p4 = p3 + vY
p5 = [0, -y, wZ2]; p6 = p5 + vY
p7 = [x, -y, 0.75 * wZ]; p8 = p7 + vY
p9 = [x + 2 * R, 0, wZ]
p10 = [-x, -y, wZ2 — R]
p11 = [x, -y, wZ2 + R]
arrPs = #(p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11)
for k = 1 to 2 do arrC[k].Height = wZ2 — R
for k = 5 to 6 do arrC[k].Height = wX — 2 * R
for k = 7 to 8 do arrC[k].Height = wZ2 — 2 * R
arrC[9].Height = wY — 2 * R
)
—
fn fndPs2 R wX wY wZ &arrPs2 = (
x = 0.5 * wX
y = 0.5 * wY
vY = [0, wY, 0]
wZ2 = wZ / 2
pc1 = [-x + R, -y, wZ2 — R]; pc2 = pc1 + vY
pc3 = [x — R, -y, wZ2 + R]; pc4 = pc3 + vY
pc5 = [x + R, -y, wZ — R]; pc6 = pc5 + vY
pc7 = [x + R, -y + R, wZ]; pc8 = pc7 + [0, wY — 2 * R, 0]
arrPs2 = #(pc1, pc2, pc3, pc4, pc5, pc6, pc7, pc8)
)
—
fn mkChr R wX wY wZ = (
Prps()
arrC = for k = 1 to 11 collect cylinder wireColor:clr2 radius:2
arrPs = #()
arrPs2 = #()
fndPs R wX wY wZ &arrPs
fndPs2 R wX wY wZ &arrPs2
arrC[3].Height = arrC[4].Height = sqrt ((0.5 * wX)^2 + (0.5 * wZ)^2)
for k = 10 to 11 do arrC[k].Height = wY
for k = 5 to 9 do arrC[k].Pivot = [0, 0, 0.5 * arrC[k].Height]
for k = 1 to 11 do arrC[k].Pos = arrPs[k]
for k = 3 to 4 do rotate arrC[k] -(atan (1.0 * wX / wZ)) [0, 1, 0]
for k = 5 to 6 do rotate arrC[k] 90 [0, 1, 0]
for k = 9 to 11 do rotate arrC[k] -90 [1, 0, 0]
rc = arc radius:R from:0 to:90 pie:off reverse:off pos:[0, 0, 0] \
rotation:(quat -0.5 0.5 -0.5 -0.5) wireColor:clr2 \
render_renderable:on render_displayRenderMesh:on render_useViewportSettings:off \
render_mapcoords:on render_displayRenderSettings:off render_viewport_thickness:4.0 \
render_thickness:4.0
arrRc = for k = 1 to 7 collect copy rc
arrRc.WireColor = clr2
arrRc[6].Rotation = quat 0 0 -0.707107 0.707107
arrRc[7].Rotation = quat 0 0 0 1
insertItem rc arrRc 1
arrNg = #(0, 0, 180, 180, 0, 0, 0, 0)
for k = 1 to 8 do (
rotate arrRc[k] arrNg[k] [0, 1, 0]
arrRc[k].Pos = arrPs2[k]
)
max tool zoomExtents
global pln = plane length:wY width:(wX — R) lengthSegs:1 widthSegs:1 \
pos:[0, 0, wZ / 2] wireColor:clr
p = arrPs[7]; p[2] = 0
global pln2 = plane length:wY width:(wZ / 2 — 2 * R) lengthSegs:1 widthSegs:1 \
pos:p wireColor:clr
rotate pln2 -90 [0, 1, 0]
)
—
fn chgChr R wX wY wZ = (
for k = 1 to 2 do arrC[k].Height = 0.5 * wZ — R
for k = 5 to 6 do arrC[k].Scale = [1, 1, (wX — 2 * R) / arrC[5].Height]
for k = 7 to 8 do arrC[k].Scale = [1, 1, (0.5 * wZ — 2 * R) / arrC[7].Height]
arrC[9].Scale = [1, 1, (wY — 2 * R) / arrC[9].Height]
arrC[9].Pos = [0.5 * wX + 2 * R, 0, wZ]
arrC[10].Pos = [-0.5 * wX, -0.5 * wY, 0.5 * wZ — R]
arrC[11].Pos = [0.5 * wX, -0.5 * wY, 0.5 * wZ + R]
arrPs2 = #()
fndPs2 R wX wY wZ &arrPs2
for k = 1 to 8 do arrRc[k].Pos = arrPs2[k]
arrRc.Radius = R
pln.Width = wX — 2 * R
pln2.Width = 0.5 * wZ — 2 * R
)
—
rollout rChr «Chair» width:120 height:100 (
spinner spnR «R » pos:[15,5] width:100 height:20 range:[5,15,1] type:#integer
colorPicker theClr «Color » pos:[15,30] width:100 height:20 color:clr modal:true
button btnNmt «Animation» pos:[15,55] width:100 height:20 toolTip:»Play animation»
button btnCls «Close» pos:[15,80] width:100 height:20 toolTip:»Close Dialog»
on spnR changed val do chgChr val wX wY wZ
on theClr changed newClr do (
clr = newClr
pln.WireColor = newClr
pln2.WireColor = newClr
)
on btnNmt pressed do (
animationRange = interval 0f 100f
timeConfiguration.PlaybackLoop = false
with redraw off (
animate on (
at time 0f chgChr spnR.Range[1] wX wY wZ
at time 50f chgChr spnR.Range[2] wX wY wZ
at time 100f chgChr 10 wX wY wZ
)
)
max tool zoomExtents
playAnimation()
with redraw off (
sliderTime = 0f
chgChr 10 wX wY wZ
)
spnR.Value = 10
)
on btnCls pressed do closeRolloutFloater rlFlt
)
—
function opnRlFlt = (
if rlFlt != undefined then closeRolloutFloater rlFlt
rlFlt = newRolloutFloater «Chair» (rChr.Width + 35) (rChr.Height + 35) 50 50
addRollout rChr rlFlt rolledUp:false
rChr.spnR.Value = 10
)
—
mkChr 10 wX wY wZ
opnRlFlt()
Запуск программы
Запуск программы выполняется в 3ds Max в следующем порядке:
- Открыть редактор кода (меню MAXScript – MAXScript Editor).
- Перейти в открывшийся диалог и при необходимости создать новую вкладку (Ctrl + N).
- Скопировать код в чистую вкладку редактора.
- Позиционироваться в любом месте скопированного кода и нажать Ctrl + E, либо воспользоваться меню редактора Tools – Evaluate All.
- Употребить появившийся диалог (рис. 4) для управления моделью стула, которая отобразится в сцене непосредственно перед открытием диалога.

Рис. 4. Управляющий диалог Chair
Описание программы
Построение стула обеспечивает функция mkChr, которая принимает в качестве параметров значения радиуса скруглений, длину, ширину и высоту стула – это соответственно параметры R, wX, wY и wZ. Стул состоит из 11 цилиндров (примитив Cylinder), 8 дуг (примитив Arc) и двух плоскостей (примитив Plane). Последние употребляются для отображения сиденья и спинки стула.
Переменные wX, wY и wZ объявлены как глобальные, что позволяет применять их в обработчике on btnNmt pressed управляющего диалога Chair (идентификатор rChr).
Цилиндры хранит массив arrC; номера цилиндров, то есть их индексы в массиве arrC, показаны на рис. 5, а.
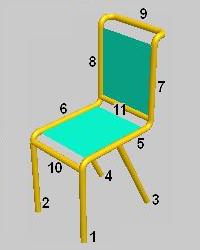 |
 |
| а | б |
|
Рис. 5. Нумерация компонентов модели стула: а – нумерация цилиндров; б – нумерация дуг |
Дуги хранятся в массиве arrRc; их индексы в этом массиве показаны на рис. 5, б.
Плоскости для сиденья и спинки имеют в программе соответственно идентификаторы pln и pln2. Эти имена являются глобальными и поэтому доступны в обработчиках диалога Chair.
Перед построением модели функцией Prps удаляются все элементы сцены и устанавливаются требуемые параметры сеанса – это тип единиц измерения, число видовых портов (4), активный видовой порт (4) и его тип (Perspective). Кроме того, в этом видовом порте устраняется изображение сетки и выполняется команда max tool zoomExtents.
Координаты базовых точек цилиндров и дуг вычисляются соответственно функциями fndPs и fndPs2, принимающими вдобавок к параметрам R, wX, wY и wZ соответственно массивы arrPs и arrPs2. В эти массивы названные функции записывают необходимые для построения примитивов координаты их базовых точек. Нумерация базовых точек отвечает показанным на рис. 5 нумерациям цилиндров и дуг.
Параметризация модели обеспечивается функцией chgChr, которая вызывается обработчиком on spnR changed при изменении счетчика R (spinner spnR) диалога Chair. Также эта функция применяется при создании ключей анимации (кнопка Animation диалога Chair).
Функция принимает параметры R, wX, wY и wZ. Параметр R является изменяемым, и его значение берется равным показанию счетчика R диалога. Прочие параметры после запуска программы не изменяются.
Получив новое значение радиуса, функция chgChr:
- изменяет высоту цилиндров 1 и 2 (свойство Height цилиндра);
- соответствующим образом масштабирует цилиндры 5 – 9 (свойство Scale цилиндра);
- изменяет положение цилиндров 9, 10 и 11 (свойство Pos цилиндра), смещая позицию цилиндров 10 и 11 в начало, а цилиндр 9 в конец соответствующих дуг модели;
- изменяет координаты центра каждой дуги (свойство Pos дуги); для этой цели, как и при создании модели, выполняется обращение к функции fndPs2;
- изменяет значение радиуса каждой дуги (свойство Radius дуги);
- модифицирует ширину сиденья и спинки (свойство Width плоскостей pln и pln2).
В рассматриваемой модели масштабирование цилиндра будет вызывать надлежащий эффект, если базовая точка цилиндра (свойство Pivot) расположена в его центре, а не в центре основания, как это предусмотрено по умолчанию. Эта проблема решается при создании модели функцией mkChr за счет употребления следующего кода:
for k = 5 to 9 do arrC[k].Pivot = [0, 0, 0.5 * arrC[k].Height]
Таким образом, функция chgChr обеспечивает получение экземпляра модели, отвечающего принятому функцией значению радиуса скругления R. Все преобразования выполняются исходя из неизменности габаритов стула и положения его сиденья. Единственными неизменяемыми компонентами модели являются цилиндры 3 и 4, отображающие задние ножки стула.
Кроме обработчика on spnR changed, вызываемого при изменении показания счетчика R, диалог Chair (см. рис. 4) содержит обработчики on theClr changed, on btnNmt pressed и on btnCls pressed do, выполняемые соответственно при нажатии на полосу с цветом (элемент colorPicker), на кнопку Animation (элемент button btnNmt) и Close (элемент button btnCls).
Ключи анимации рассчитываются в точках 0f, 50f и 100f временной шкалы после нажатия на кнопку Animation диалога Chair: выполняется обработчик on btnCls pressed do, в котором трижды вызывается функция chgChr. После воспроизведения анимации (метод playAnimation) временная шкала устанавливается в точку 0f и вновь вызывается функция chgChr со значением параметра R, равным 10. Это обеспечивает появление начального образа стула. Это же значение радиуса скругления устанавливается и в счетчике R диалога (spnR.Value = 10).
Заключение
Параметрические модели требуют дополнительных издержек при их создании. Поэтому вопрос о целесообразности параметризации модели решается с учетом предполагаемых выгод.
Издержки связаны с необходимостью:
- структуризации модели и сохранения в ней параметров, влияющих на ее геометрию;
- поиска зависимостей между параметрами;
- реализации этих зависимостей (как правило, с привлечением MAXScript).
Основной эффект параметризации – это возможность получения модифицированного экземпляра модели, за счет изменения небольшого числа параметров. Так, параметрическая модель кузова автомобиля может обеспечить пересчет всех компонентов кузова при изменении геометрии двери или иной части кузова.
Также параметрические модели несложно снабдить надлежащим, более удобным пользовательским интерфейсом, обеспечивающим управление отдельными параметрами модели и, значит, моделью в целом.
Кроме того, параметризация предоставляет дополнительные возможности для анимации модели, что, в частности, существенно при создании мультимедийных приложений.
Источники
- Autodesk® 3ds Max® 2009 MAXScript Reference.
- Бартеньев О. В. Программирование модификаторов 3ds Max. Учебно-справочное пособие. – М.:Физматкнига, 2009. – 341 с.
Список примеров
FILED UNDER : IT