admin / 26.06.2018
Найдите наибольшую часть числа 3591 при разбиении
Содержание
Системы счисления, перевод в систему счисления
Десятичное число 3591
-
- 3591 в шестнадцатеричной системе счисления
- E07
-
- 3591 в двоичной системе счисления
- 111000000111
-
- 3591 в восьмеричной системе счисления
- 7007
Шестнадцатеричное число E07
-
- E07 в десятичной системе
- 3591
-
- E07 в двоичной системе
- 111000000111
-
- E07 в восьмеричной системе
- 7007
Двоичное число 111000000111
-
- 111000000111 в десятичной системе
- 3591
-
- 111000000111 в шестнадцатеричной системе
- E07
-
- 111000000111 в восьмеричной системе
- 7007
Восьмеричное число 7007
-
- 7007 в десятичной системе
- 3591
-
- 7007 в шестнадцатеричной системе
- E07
-
- 7007 в двоичной системе
- 111000000111
Основные арифметические и алгебраические свойства
-
- Число 3591 на русском языке, number in Russian, число 3591 прописью:
- три тысячи пятьсот девяносто один
-
- Четность
- Нечетное число 3591
-
- Разложение на множители, делители числа 3591
- 3, 3, 3, 7, 19, 1
-
- Простое или составное число
- Составное число 3591
-
- Числа делящиеся на целое число 3591
- 7182, 10773, 14364, 17955, 21546, 25137, 28728, 32319
-
- Число 3591 умноженное на число два
- 7182
-
- 3591 деленное на число 2
- 1795.5
-
- Список 8-ми простых чисел перед числом
- 3583, 3581, 3571, 3559, 3557, 3547, 3541, 3539
-
- Сумма десятичных цифр
- 18
-
- Количество цифр
- 4
-
- Десятичный логарифм 3591
- 3.5552154051261
-
- Натуральный логарифм 3591
- 8.1861859942261
-
- Это число Фибоначчи?
- Нет
-
- Число на 1 больше числа 3591,
следующее число - число 3592
- Число на 1 больше числа 3591,
-
- Число на 1 меньше числа 3591,
предыдущее число - 3590
- Число на 1 меньше числа 3591,
Степени числа, корни
-
- 3591 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 12895281
- 3591 во второй степени (в квадрате)
-
- В третьей степени (в кубе, 3591 в степени 3, x³) равно
- 46306954071
-
- Корень квадратный из 3591
- 59.924953066315
-
- Корень кубический из числа 3591 =
- 15.313406166004
Тригонометрические функции, тригонометрия
-
- Синус, sin 3591 градуса, sin 3591°
- -0.156434465
-
- Косинус, cos 3591 градуса, cos 3591°
- 0.9876883406
-
- Тангенс, tg 3591 градуса, tg 3591°
- -0.1583844403
-
- Синус, sin 3591 радиан
- -0.15892028863404
-
- Косинус, cos 3591 радиан
- -0.98729141688788
-
- Тангенс, tg 3591 радиан равно
- 0.16096593763064
-
- 3591 градус, 3591° =
- 62.674773439116 радиан
-
- 3591 радиан =
- 205749.14423148 градуса, 205749.14423148°
Контрольные суммы, хэши, криптография
-
- MD-5 хэш(3591)
- 9001ca429212011f4a4fda6c778cc318
-
- CRC-32, CRC32(3591)
- 3189777064
-
- SHA-256 hash, SHA256(3591)
- 572878043beff72a7ae455785619593dac4a462771c18335de2a49a010efbc47
-
- SHA1, SHA-1(3591)
- 38f61a1d750a79773ac539615864e95597e9a66c
-
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(3591)
- fd4d20ab88fda532153f0160cde156cdc1281821c1a41a54f27dbd0911ad98e9
-
- Base64
- MzU5MQ==
Языки программирования
-
- C++, CPP, C значение 3591
- 0x000E07, 0xE07
-
- Delphi, Pascal значение числа 3591
- $000E07
Дата и время
-
- Конвертация UNIX timestamp 3591 в дату и время
-
- UTC
- в Москве, Россия
- в Лондоне, Великобритания
- в Нью-Йорке, США
Интернет
-
- Конвертация в IPv4 адрес Интернет
- 0.0.14.7
-
- 3591 в Википедии:
- 3591
Другие свойства числа
-
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/3591
-
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/xE07
-
- Номер телефона
- 35-91
-
- Телефонный код страны
- +3591
Цвет по числу 3591, цветовая гамма
-
- html RGB цвет 3591, 16-ричное значение
- #000E07 — (0, 14, 7)
-
- HTML CSS код цвета #000E07
- .color-mn { color: #000E07; }
.color-bg { background-color: #000E07; }
Цвет для данного числа 3591
Здесь вы можете изменить составляющую цвета для данного числа 3591 или цвета 000E07:
Коррекционные упражнения
Тема: Количественная модель числа
Цель: Учить соотносить число с его количественной моделью.
Упражнение 1.
Цель: Уточнять понимание слова и пары, учить образовать множество в соответствии с заданной количественной характеристикой. Материал: счетные палочки.
Задание: Достаньте из коробочки пару палочек одного цвета.
Вопрсы: Что значит пара? Какого она цвета?
Возьмите ещё одну палочку, но другова цвета, что у вас.
Вопрсы:Что это значит? Сколько теперь у вас палочек?
Упражнение 2.
Цель: Актуализировать умения соотносить число и количество.
Задание: Покажите, сколько пальцев на одной руке.
Вопрсы: Сколько палочек? Сколько пальцев ты показываешь? Сколько пальцев показывает Петя и Катя?
Упражнение 3.
Цель: Актуализировать умения соотносить число и количество.
Задание: А пальцев на одной руке сколько? Анна другой руке? Давайте посчитаем вместе, (при счете дети дотрагиваются до каждого пальца). А на двух руках, кто знает сколько пальцев? Кто может посчитать?
Упражнение 4.
Цель: Актуализировать умения соотносить число и количество.
Задание: Сколько палочек у вас на столе? Возьмите ещё одну палочку и положите её сверху горизонтально. Сколько стало палочек?
Сосчитайте. На что похожа эта фигура? (на ворота и букву «П»)
Кто знает слова, начинающиеся на эту букву? (дети называют слова, начинающиеся на букву «П»).
Упражнения 5.
Цель: Учить соотносить число и его количественную модель.
Материал: Тетрадь.
Задание: Найди фишку с цифрой, обозначающую количество квадратов на рисунке. Выложи под рисунком столько треугольников, сколько больших кружков ты запросил. Нарисуй столько палочек, сколько маленьких кружков на рисунке.

Упражнение 6.
Цель: Учить соотносить число и его количественную модель.
Задание: Правильно найди на рамке нужные треугольники. Одинаковые треугольники раскрась одним цветом. Сосчитай все треугольники на рисунке. Сосчитай все четырехугольники и закрась цифру соответствующую их количеству.


Упражнение 7.
Цель: Актуализировать умения соотносить число и количество. Сложи такую машину из фигурок. Нарисуй нужные детали на цветной бумаге, используя рамку, вырежи их и сделай аппликацию » Машина».

Сколько треугольников? Закрась нужную цифру.

Сколько кругов?

Сколько квадратов?

Сложи такую же машину из фигурок, чтобы она ехала в другую сторону. Сосчитай все треугольники в двух машинах; все круги; все квадраты. Найди фишки с разными цифрами.

Упражнение 8.
Цель: Актуализировать умения соотносить число и количество.

Какие фигуры на рисунке только по две? Раскрась одинаковые фигурки одним цветом. Сколько треугольников всего вместе? Раскрась нужную цифру:

Сложи похожую картинку из фигурок (для туловища используй квадраты).
Упражнение 9.
Цель: Актуализировать умения соотносить число и количество. Сложи бабочку из треугольников, сколько треугольников понадобилось?
Поставь фишку с цифрой:

Используя столько же треугольников, сложи цветок. Попробуй придумать свою композицию. Используй детали мозаики.

Упражнение 10.
Цель: Актуализировать умения соотносить число и количество. Вырежи детали со следующей страницы и приклей на рисунок «Заяц». Кружки для лапок и щек вырежи из цветной бумаги, используя рамку, и приклей на рисунок. Мелкие детали раскрась фломастером.

Сколько треугольников на рисунке?
Сколько больших кругов?
Сколько маленьких кругов?
Естественные науки / Дискретная математика / 3.2. Разбиения чисел
Разбиением натурального числа n на k слагаемых называется последовательность таких положительных натуральных чисел ( a1, a2, …, ak), что
n = a1 + a2 + …+ ak, k>0, a1³ a2³…³ ak > 0.
Пусть P(n,k) – число разбиений n на k слагаемых. Тогда число всех разбиений равно:
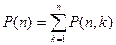 , n>0.
, n>0.
Полагаем по определению P(0) = P(0,0) = 1.
Пример 1
P(5) = 7:
5 = 5,
5 = 4 + 1;
5 = 3 + 2;
5 = 3 + 1 + 1;
5 = 2 + 2 + 1;
5 = 2 + 1 + 1 + 1;
5 = 1 + 1 + 1 + 1 + 1.
Замечание
Каждое разбиение можно наглядно представить с помощью диаграммы Ферреса, которая для n = a1 + a2 + …+ ak состоит из k строк, а i-строка содержит ai точек. Например, для 5 = 2 + 2 + 1 диаграмма Ферреса имеет вид (рис. 3.1, а). Если отразить диаграмму относительно ее главной диагонали, то мы получим диаграмму Ферреса, которая называется сопряженной (рис. 3.1, б). Она будет соответствовать разбиению 5 = 3 + 2.
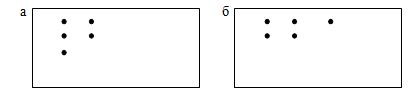
Рис.
3.1. Диаграммы Ферреса
Лемма 1
Число разбиений P(n) равно количеству решений
(l1, l2, …, ln )
уравнения l1×1 + l2×2 + …+ ln×n = n.
Доказательство
Если среди чисел a1 ³ a2³ …³ ak разбиения числа n имеется l1 единиц, l2двоек, …, ln — n-ок, то получаем решение уравнения.
Ясно, что это соответствие взаимно однозначно.
Обозначим через Ph(n) количество разбиений числа n на слагаемые, не большие чем h.
Теорема 1
Производящая функция последовательности чисел разбиений Ph(0), Ph (1), Ph (2), … равна:
 .
.
Доказательство
Произведение равно:
(1 +x + x2 +…)(1 + x2 + x4 +…)(1 + x3 + x6+ …)×… (1 + xh + x2h + …).
Если перемножить содержимое скобок, то получим многочлен, равный сумме одночленов 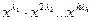 .
.
Отсюда коэффициент при xn равен числу последовательностей (l1, l2, …×, lh), для которых l1 ×1 + l2 ×2 + …+ lh ×h = n. Он будет равен числу разбиений n на слагаемые, не большие чем h.
Следствие 1
Производящая функция последовательности чисел разбиений P(0), P(1), P(2),… равна:
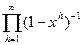 .
.
FILED UNDER : IT