Тензорное исчисление

    Тензорное исчисление, математическая теория, изучающая величины особого рода — тензоры, их свойства и правила действий над ними. Т. и. является развитием и обобщением векторного исчисления и теории матриц. Т. и. широко применяется в дифференциальной геометрии, теории римановых пространств, теории относительности, механике, электродинамике и других областях науки.

    Для описания многих физических и геометрических фактов обычно вводится та или иная система координат, что позволяет описывать различные объекты при помощи одного или нескольких чисел, а соотношения между объектами — равенствами, связывающими эти числа или системы чисел. Некоторые из величин, называемые скалярными (масса, температура и т. д.), описываются одним числом, причём значение этих величин не изменяется при переходе от одной системы координат к другой (мы рассматриваем здесь физические явления с точки зрения классической физики). Другие величины — векторные (сила, скорость и т. д.), описываются тремя числами (компонентами вектора), причём при переходе от одной системы координат к другой компоненты вектора преобразуются по определённому закону. Наряду со скалярными и векторными величинами встречаются во многих вопросах физики и геометрии величины более сложного строения. Эти величины, называемые тензорными, описываются в каждой системе координат несколькими числами (компонентами тензора), причём закон преобразования этих чисел при переходе от одной системы координат к другой более сложен, чем для векторов (точные определения будут даны ниже). При введении координатной системы, помимо чисел, описывающих сам объект или физическое явление, появляются числа, описывающие его связь с выбранной системой координат. Рассмотрим, например, совокупность чисел J_ij (i, j = 1, 2, 3), где J_ij — осевой момент инерции твёрдого тела относительно оси X_i, a J_ij, (при i¹j) — центробежные моменты инерции, взятые с обратным знаком. При переходе от одной системы координат к другой осевой момент инерции J_ii меняется (так как меняется положение оси xi относительно тела), а потому J_ii не может рассматриваться как физическая величина, имеющая независимый от выбора системы координат смысл. Это находит своё выражение, например, в том, что знание J_ii в одной системе координат не позволяет найти J_ii в другой системе координат. В то же время совокупность всех чисел J_ij имеет смысл, независимый от выбора координатной системы. Знание всех чисел J_ij в одной системе прямоугольных координат позволяет найти их в любой другой системе прямоугольных координат по формуле 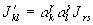( и

    Т.о., одной из основных задач Т. и. является нахождение аналитических формулировок законов механики, геометрии, физики, не зависящих от выбора координатной системы.

    Тензоры

    Форма выглядит следующим образом:

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.

Тензорной алгеброй линейного пространства V обозначается T V называется алгебра тензоров любого ранга над V с операцией тензорного умножения

Также тензорной алгеброй называется соответствующий раздел линейной алгебры то есть раздел, занимающийся тензорами, определёнными над одним линейным пространством, в отличие от тензорного анализа, занимающегося тензорными полями, заданными на касательном расслоении многообразия и дифференциальными соотношениями для этих полей

Содержание

• 1 Определение
• 2 Универсальное свойство и функториальность
• 3 Некоммутативные многочлены
• 4 Факторалгебры
• 5 Вариации и обобщения
• 6 Ссылки
• 7 См также

Определениеправить

Пусть V — векторное пространство над полем K Для любого натурального числа k определим k-ую тензорную степень V как тензорное произведение V на себя k раз:

T k V = V ⊗ k = V ⊗ V ⊗ ⋯ ⊗ V V=V^=V\otimes V\otimes \cdots \otimes V

Таким образом, TkV состоит из всех тензоров над V ранга k Будем считать, что T0V — это основное поле K одномерное векторное пространство над собой

Определим TV как прямую сумму TkV для всех k = 0,1,2,…

T V = ⨁ k = 0 ∞ T k V = K ⊕ V ⊕ V ⊗ V ⊕ V ⊗ V ⊗ V ⊕ ⋯ ^T^V=K\oplus V\oplus V\otimes V\oplus V\otimes V\otimes V\oplus \cdots

Умножение в TV определяется задаваемым тензорным произведением каноническим изоморфизмом:

T k V ⊗ T ℓ V → T k + ℓ V V\otimes T^V\to T^V

который потом продолжается по линейности на всю TV Такое умножение превращает тензорную алгебру TV в градуированную алгебру

Универсальное свойство и функториальностьправить

Тензорная алгебра TV — это свободная алгебра векторного пространства V Как и для любой другой свободной конструкции, функтор Т является левым сопряженным функтором забывающего функтора который в данном случае отпраляет К-алгебру в её векторное пространство Тензорная алгебра удовлетворяет следующему универсальному свойству, которое формализует утверждение, что это наиболее общая алгебра, содержащая пространство V:

Любое линейное отображение f : V → A пространства V над полем К в алгебру A над K может быть единственным образом продолжено до гомоморфизма алгебр f ¯ : T V → A :TV\to A Это утверждение выражается коммутативной диаграммой:

где i — каноническое вложение V в TV Тензорную алгебру можно определить как единственную с точностью до изоморфизма алгебру, обладающую таким свойством, хотя необходимо ещё явно показать, что такая алгебра существует

Приведенное выше универсальное свойство показывает, что тензорная алгебра функториальна, то есть T — это функтор из категории K-Vect векторных пространств над K в категорию K-Alg K-алгебр Функториальность Т означает, что любое линейное отображение из V в W может быть единственным образом продолжено до гомоморфизма из алгебры TV в TW

Некоммутативные многочленыправить

Если размерность V конечна и равна n, то тензорную алгебру можно рассматривать как алгебру многочленов над K с n некоммутативными переменными Базисным векторам V соответствуют некоммутативные переменные, причем их умножение будет ассоциативным, дистрибутивным и K-линейным

Заметим, что алгебра многочленов над V — это не T V , а T V ∗ : однородная линейная функция на V является элементом сопряженного пространства V ∗

Факторалгебрыправить

В силу общности тензорной алгебры многие другие важные алгебры пространства V можно получить, накладывая определенные ограничения на образующие элементы тензорной алгебры, то есть строя факторалгебры от TV Например, так можно построить внешнюю алгебру, симметрическую алгебру и алгебру Клиффорда

Вариации и обобщенияправить

Конструкция тензорной алгебры над линейным пространством естественно обобщается до тензорной алгебры над модулем M над коммутативным кольцом Если R — некоммутативное кольцо, можно построить тензорное произведение для любых R-бимодулей над M Для обычных R-модулей оказывается невозможным построить кратное тензорное произведение

Ссылкиправить

• Винберг Э Б Курс алгебры — М:Издательство «Факториал Пресс» — 2002, ISBN 5-88688-060-7

См такжеправить

• Алгебра Клиффорда
• Внешняя алгебра
• Симметрическая алгебра

---

Тензорная алгебра Информация о

---

Тензорная алгебра
Тензорная алгебра

Тензорная алгебра Информация Видео

Тензорная алгебра Просмотр темы.

Тензорная алгебра что, Тензорная алгебра кто, Тензорная алгебра объяснение

There are excerpts from wikipedia on this article and video

---

Тензорное исчисление, математическая теория, изучающая величины особого рода — тензоры, их свойства и правила действий над ними. Т. и. является развитием и обобщением векторного исчисления и теории матриц. Т. и. широко применяется в дифференциальной геометрии, теории римановых пространств, теории относительности, механике, электродинамике и других областях науки.

  Для описания многих физических и геометрических фактов обычно вводится та или иная система координат, что позволяет описывать различные объекты при помощи одного или нескольких чисел, а соотношения между объектами — равенствами, связывающими эти числа или системы чисел. Некоторые из величин, называемые скалярными (масса, температура и т. д.), описываются одним числом, причём значение этих величин не изменяется при переходе от одной системы координат к другой (мы рассматриваем здесь физические явления с точки зрения классической физики). Другие величины — векторные (сила, скорость и т. д.), описываются тремя числами (компонентами вектора), причём при переходе от одной системы координат к другой компоненты вектора преобразуются по определённому закону. Наряду со скалярными и векторными величинами встречаются во многих вопросах физики и геометрии величины более сложного строения. Эти величины, называемые тензорными, описываются в каждой системе координат несколькими числами (компонентами тензора), причём закон преобразования этих чисел при переходе от одной системы координат к другой более сложен, чем для векторов (точные определения будут даны ниже). При введении координатной системы, помимо чисел, описывающих сам объект или физическое явление, появляются числа, описывающие его связь с выбранной системой координат. Рассмотрим, например, совокупность чисел J_ij(i, j = 1, 2, 3), где J_ij— осевой момент инерции твёрдого тела относительно оси X_i, a J_ij, (при i¹j) — центробежные моменты инерции, взятые с обратным знаком. При переходе от одной системы координат к другой осевой момент инерции J_ii меняется (так как меняется положение оси x_i относительно тела), а потому J_ii не может рассматриваться как физическая величина, имеющая независимый от выбора системы координат смысл. Это находит своё выражение, например, в том, что знание J_iiв одной системе координат не позволяет найти J_ii в другой системе координат. В то же время совокупность всех чисел J_ij имеет смысл, независимый от выбора координатной системы. Знание всех чисел J_ij в одной системе прямоугольных координат позволяет найти их в любой другой системе прямоугольных координат по формуле  ( и  — некоторые числа): здесь, как принято в Т. и., опущен знак суммы и считается, что если один и тот же индекс встречается дважды (один раз наверху, а другой раз внизу), то по нему производится суммирование, причём этот индекс принимает все возможные для него значения (в приведённом примере — значения 1, 2, 3).

Т. и., как и векторное исчисление, является математическим аппаратом, при котором исключается влияние выбора координатной системы. Это достигается тем, что задание компонент тензора в какой-либо системе координат определяет их во всех других системах координат. В Т. и. указываются методы получения соотношений между тензорами и функций от компонент тензоров, не меняющихся при переходе от одной системы координат к другой (инвариантных соотношений и инвариантов).

  Т. о., одной из основных задач Т. и. является нахождение аналитических формулировок законов механики, геометрии, физики, не зависящих от выбора координатной системы.

1. Тензоры в прямоугольных координатах. Величины, которые в каждой системе прямоугольных координат задаются в 3-мерном пространстве 3^k числами 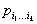(i_r = 1, 2, 3) и при замене системы координат (x₁, x₂, x₃) системой (x’₁, x’₂, x’₃) заменяются числами  по формулам:

, (1)

где 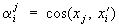, называются тензорными величинами, а определяющие их системы чисел — тензорами в прямоугольных координатах (иногда тензорами называют также и сами тензорные величины). Число k называется валентностью (рангом) тензора, числа 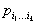— его компонентам и (координатами). Аналогичным образом определяются тензоры в пространстве любого числа измерений.

  Примеры тензоров: если координаты вектора а обозначить a_i (i = 1, 2, 3), то числа а, образуют тензор первой валентности. Любым двум векторам а = {a_i}и b ={b_i} соответствует тензор с компонентами p_ij = a_i. b_j. Этот тензор называется диадой. Если a (x₁, x₂, x₃) — некоторое векторное поле, то каждой точке этого поля соответствует тензор с компонентами . Он называется производной вектора а = {ai} по вектору r {x₁, x₂, хз} (обозначается также через ). Упомянутая выше совокупность чисел J_ij образует тензор второй валентности (тензор инерции).

2. Тензоры второй валентности. В приложениях Т.

и. к механике, кроме тензоров первой валентности (векторов), чаще всего встречаются тензоры второй валентности.

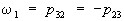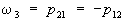
  Если p_ij = p_ji, то тензор называется симметрическим, а если p_ij = –p_ji, то — кососимметрическим (антисимметрическим). Симметрический тензор имеет шесть существенных компонент, а кососимметрический — три: ; ; 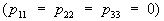. При этом компоненты w₁, w₂, w₃ преобразуются как компоненты псевдовектора (см. Осевой вектор). Вообще псевдовекторы (угловую скорость, векторное произведение двух векторов и др.) можно рассматривать как кососимметрические тензоры второй валентности. Далее, если в любой системе координат принять 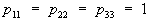, , 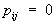, 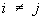то получится тензор, называемый единичным тензором. Компоненты этого тензора обозначаются при помощи Кронекера символаd_ij. Тензоры инерции, напряжения, единичный тензор — симметрические. Всякий тензор единственным образом разлагается на сумму симметрических и кососимметрических тензоров. Если а (r) — вектор смещения частиц упругого тела при малой деформации, то симметрическая часть  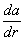называется тензором деформации; кососимметрическая часть  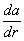соответствует псевдовектору  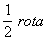(см. Вихрь векторного поля).

Тензор 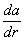 является симметрическим только в том случае, когда поле а (r) потенциально (см. Потенциальное поле). Разложение тензора  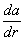на симметрические и кососимметрические части соответствует разложению относительного смещения da на чистую деформацию и на поворот тела как целого.

  Инвариантами тензора называются функции от его компонент, не зависящие от выбора координатной системы. Примером инварианта является след тензора p₁₁ + p₂₂ + p₃₃. Так, для тензора инерции он равен удвоенному полярному моменту инерции относительно начала координат, для тензора 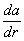 —  дивергенции векторного поля a (r) и т. д

3. Тензоры в аффинных координатах. Для многих задач приходится рассматривать тензорные величины в аффинных координатах (косоугольных координатах с различными единицами длины по разным осям). Положение одной аффинной системы координат относительно другой может быть описано двумя различными системами чисел: числами 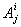 равными компонентам векторов 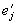. нового базиса относительно векторов  старого базиса, и числами 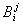, равными компонентам векторов  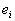относительно базиса 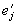. В соответствии с этим бывают тензоры различного вида: в законы преобразования одних из них входят числа , а в законы преобразования других — числа . Встречаются и тензоры, в законы преобразования которых входят как числа , так и числа 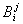. Тензоры первого вида называются ковариантными, второго — контравариантными и третьего — смешанными тензорами. Более точно, (r + х)-валентным смешанным тензором s раз ковариантным и r раз контравариантным. называют совокупность 3^r+s чисел , заданную в каждой системе аффинных координат и преобразующуюся при переходе от одной системы координат к другой по формулам:

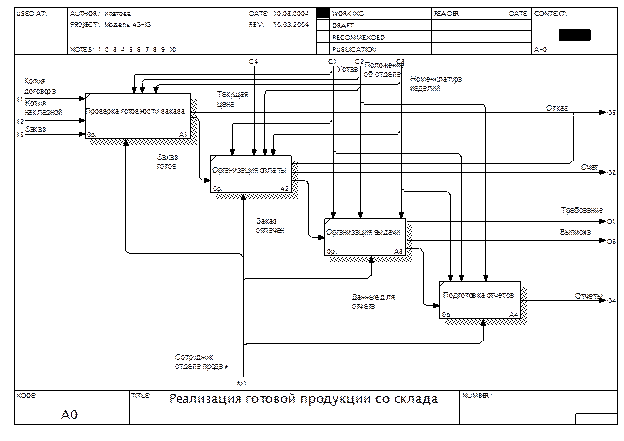
При рассмотрении прямоугольных координат не приходится различать ковариантные (нижние) и контравариантные (верхние) индексы тензора, так как для двух таких систем координат .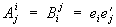

  Коэффициенты уравнения поверхности второго порядка  образуют ковариантный тензор валентности 2, а элементы 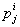 матрицы линейного преобразования — тензор, 1 раз ковариантный и 1 раз контравариантный. Система трёх чисел x₁, x₂, x₃, преобразующихся как координаты вектора x = xⁱe_i, образует 1 раз контравариантный тензор, а система чисел, преобразующихся как скалярное произведение x_i = xe_i, образует 1 раз ковариантный тензор. Относительно преобразования аффинных координат символ Кронекера  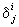является смешанным тензором (поэтому, в отличие от пункта 2, здесь пишут один индекс сверху, другой — снизу). Совокупность чисел g_ij = e_ie_j, где e_i — векторы базиса, образует тензор, называемый ковариантным метрическим тензором. Длина любого вектора пространства   х = xiei равна 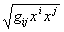, а скалярное произведение двух векторов х и у равно g_ijxⁱy^j. Совокупность величин g^ij таких, что 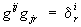, образует тензор, который называется контравариантным метрическим тензором.

  Дословно, так же как и в трёхмерном пространстве, определяются тензоры в n-мерном пространстве.

Важным примером тензоров в n-мерном пространстве являются совокупности компонент поливекторов.

  Порядок следования индексов существенным образом входит в определение тензора, то есть при перестановке индексов компоненты тензора, вообще говоря, меняются. Тензор называется симметрическим по данной совокупности индексов (одного и того же уровня), если при перестановке любых двух индексов этой совокупности он не меняется. Если же при такой перестановке компоненты тензора меняют знак, то он называется кососимметрическим по этой совокупности индексов. В более общем смысле условием симметрии тензора называют любую инвариантную линейную зависимость между его компонентами.

4. Действия над тензорами. Существуют четыре основные операции над тензорами: сложение тензоров, умножение тензоров, свёртывание тензоров по двум или более индексам и перестановка индексов тензора. Так как тензор задаётся своими компонентами в различных системах координат, то действия над тензорами задаются формулами, выражающими в каждой системе координат компоненты результата действия через компоненты тензоров, над которыми производятся действия. При этом формулы должны быть такими, чтобы в результате выполнения действия получился тензор.

  а) Сложение тензоров. Суммой двух тензоров 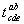 и  одинакового строения (то есть имеющих одинаковое число верхних и нижних индексов) называется тензор с компонентами

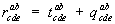
  б) Умножение тензоров. Произведением двух тензоров 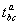 и 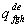 (быть может различного строения) называется тензор с компонентами 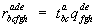. Произведение тензоров, вообще говоря, зависит от порядка сомножителей. Если один из тензоров имеет нулевую валентность (то есть является скалярной величиной l), то умножение его на другой тензор  сводится к умножению всех компонент тензора  на число l.

  в) Свёртывание тензора. Результатом свёртывания тензора 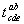 по индексам а и d (верхнему и нижнему) называется тензор 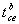, компоненты которого равны . (здесь производится суммирование по индексу i). Например, след матрицы 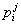 является результатом свёртывания её по индексам i и j, бискалярное произведение  тензоров  и . равно результату свёртывания их произведения по всем индексам. При полном свёртывании тензора (по всем индексам) получается инвариант.

  г) Перестановка индексов. Пусть компоненты тензора 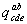 выражаются через компоненты тензора  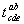формулой 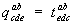. Тогда говорят, что  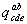получился из  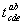перестановкой индексов с и е. При этом переставляться могут только индексы одного и того же уровня.

5. Тензорный анализ. В приложениях приходится обычно рассматривать не отдельные тензоры, а тензорные поля. Например, при изучении упругой деформации рассматривают тензоры деформации и напряжений во всех точках тела. Если в пространстве задана прямоугольная система координат, то тензорное поле Т (Р) можно рассматривать как совокупность функций , заданных в каждой точке Р (х¹, x², x³) области и преобразующихся при переходе от одной системы прямоугольных координат к другой по формулам вида (1). В этом случае частные производные компонент тензора по координатам 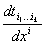 образуют также тензор, валентность которого на единицу выше валентности исходного тензора. Например, при дифференцировании скалярного поля получается поле градиента, при дифференцировании поля градиента — поле симметрического тензора второй валентности:  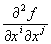и т. д.

  В тензорном анализе рассматриваются не только прямоугольные или аффинные, но и произвольные (достаточное число раз дифференцируемые) криволинейные координаты xⁱ. В окрестности каждой точки эти координаты можно заменить аффинными координатами. В качестве базисных векторов этих аффинных координат надо взять частные производные  радиус-вектораr в точке Р.

  Тогда скалярные произведения e_ie_j, будут равны значениям компонент метрического тензора g_ijв точке Р, с помощью которого длина бесконечно малого вектора 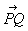, , 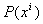 выражается формулой 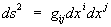. Поэтому метрика в криволинейной и прямолинейной системах координат совпадает с точностью до бесконечно малых высшего порядка. Тем самым в каждой точке пространства вводится своя (локальная) система аффинных координат, относительно которой и задаются компоненты тензорного поля в этой точке. При переходе от одной системы криволинейных координат (x’,…, x_n)к другой (y’,…, yⁿ) локальная система координат в каждой точке меняется, причём базисные векторы преобразуются по формулам 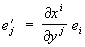. Иными словами, коэффициенты линейного преобразования  будут различными в разных точках и равны ; точно так же матрица  состоит из выражений . Поэтому тензорным полем относительно криволинейных координат. называют совокупность функций 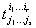,заданных в каждой точке области для системы криволинейных координат и преобразующихся при переходе от одной системы криволинейных координат к другой по формулам (2), где положено 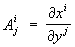, 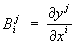. В рассматриваемом случае частные производные компонент поля по координатам xⁱ уже не образуют тензорного поля. Это объясняется тем, что при переходе от одной точки к другой изменяются не только компоненты тензора, но и локальная координатная система, к которой этот тензор относится. Поэтому при определении изменения тензора надо учитывать не только изменение компонент тензора при переходе от точки Р (xi) к бесконечно близкой ей точке Q (x’ + dxⁱ), но и изменение локальной координатной системы. Иными словами, компоненты приращения тензора нельзя считать равными приращениям его компонент. Например, для векторных полей u (P), где u имеет контравариантные компоненты u; приращение векторного поля равно (с точностью до бесконечно малых высшего порядка) выражению . Здесь через  обозначены так называемые символы Кристоффеля (см. Кристоффеля символ), связанные с метрическим тензором  соотношением

.

Отметим, что сами символы Кристоффеля не являются тензорами.

Слагаемое  учитывает зависимость компонент приращения тензора от приращения его компонент, а слагаемое 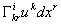 — зависимость компонент приращения тензора от изменения системы координат при переходе от точки к точке.

  Вектор  называется ковариантным (или абсолютным) дифференциалом векторного поля u (Р), а совокупность величин

.

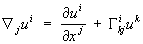— ковариантной (или абсолютной) производной этого поля. Аналогично этому ковариантная производная ковариантного векторного поля равна

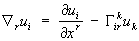
Для тензорного поля  ковариантная производная определяется формулой:

.

Ковариантная производная тензорного поля образует тензорное поле, имеющее на одну ковариантную валентность больше, чем исходное поле. В частном случае, когда криволинейные координаты являются прямоугольными, ковариантное дифференцирование тензорных полей переходит в обычное, то есть в операцию образования поля 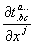 . В этом случае символы Кристоффеля равны нулю.

  Правила ковариантного дифференцирования (для суммы и произведения тензоров) совпадают с правилами обычного дифференцирования. Ковариантное дифференцирование перестановочно со свёртыванием. Имеет место также теорема о перестановке порядка ковариантного дифференцирования, то есть . Отметим, что ковариантная производная метрического тензора  равна нулю.

6. Историческая справка.Возникновение Т. и. было подготовлено в 19 в. развитием теории алгебраических форм, с одной стороны, и теории квадратичных дифференциальных форм — с другой. Исследования в области теории дифференциальных квадратичных форм были непосредственно связаны с дифференциальной геометрией: с геометрией поверхностей (К. Гаусс) и с геометрией многомерного метрического пространства (Б. Риман). Современную форму Т. и. придал итальянский математик Г. Риччи-Курбастро, поэтому Т. и.

Научный форум dxdy

иногда называется исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого распространения. Внимание к ним возросло после появления (1915—16) общей теории относительности А. Эйнштейна, математическая часть которой целиком основана на Т. и.

 

  Лит.: Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9 изд., М., 1965; Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; Схоутен Я. А., Тензорный анализ для физиков, пер. с англ., М., 1965; Мак-Коннел А.-Д., Введение в тензорный анализ, пер.

с англ., М., 1963; Сокольников И. О., Тензорный анализ, пер. с англ., М., 1971.

  По материалам одноимённой статьи из 2-го изд. БСЭ.

Тензорный метод

Тензорный метод анализа для расчета сложных систем (электрических, механических и др.) был разработан Г.Кроном, который назвал его диакоптикой.

Термин «диакоптика» происходит от греческого слова «копто», озночающего «разрывать» или «разделять на части» и приставки «диа», которая усиливает значение следующего за ней слова. Согласно диакоптике, т.е. методу исследования сложных систем по частям, реальные физические системы можно разделить на части (элементарные или примитивные цепи), рассчитываемые по отдельности, как если бы остальные части системы не существовали. Затем частные решения соединяются шаг за шагом до тех пор, пока не будет получено решение для всей системы.

Рассмотрим некоторую цепь общего вида, в которой действуют источники

напряжения и тока, а между отдельными ветвями существует магнитная связь (взаимоиндукция).

Пусть в ветвях схемы цепи протекают неизвестные токи . Выбираем в качестве вспомогательных неизвестных токи хорд (ветвей связи графа данной цепи). Обозначим эти токи, которые могут трактоваться как контурные, через … .

Контурные точки можно рассматривать как координаты вектора в -мерном пространстве (или, проще, пространстве .

Токи ветвей можно рассматривать как координаты некоторого другого вектора и -мерном пространстве (или, проще, пространстве ). Введенные векторы токов выражаются матрицами

Расположение индексов вверху означает, что эти векторы контрварианты. Токи ветвей всегда можно выразить с помощью I-го закона Кирхгофа или, что одно и то же, приравнять их сумме контурных токов, протекающих в ветвях.

В результате получается следующее выражение:

Каждый коэффициент равен 0, +1 или -1 в зависимости от наличия тока в рассматриваемой ветви и от совпадения его направления с принятым для данной ветви за положительное.

Таблица коэффициентов может рассматриваться как матрица преобразования от , т.е.

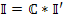
Введенная матрица , называемая также матрицей связи или соединений, при соответсвующем выборе дерева графа цепи совпадает с ранее рассмотренной транспортированной матрицей главных контуров, т.е.

.

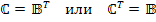Для произвольной обобщенной ветви на рис.16 в соответствии с принятыми обозначениями для ветви уравнение можно записать в виде

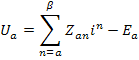
Матрицы, составленные из напряжений и э.д.с. ветвей

,

представляют собой ковариантные векторы (отмечены нижними индексами). Расходуемая в цепи мощность

,

откуда следует, что матрица

представляет собой дважды ковариантный тензор (тензор полных сопротивлений). Диагональные члены представляют собой собственные полные сопротивления ветвей, а внедиагональные определяются электромагнитной связью ветвей.

В обратимых цепях . Например, при взаимоиндукции с коэффициентом двух ветвях

(при решении конкретных задач необходимо придерживаться правил знаков для согласного и встречного включений).

Обобщая соотношение для всех ветвей, запишем

ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>»>

Рассмотрим преобразование, позволяющее перейти от пространства к пространству . Оно определенно матрицей связи

Здесь — матрицы, представляющие соответствующие тензорные величины в пространстве .

Соотношение, связывающее тензорные величины, не зависит от выбора системы координат и в пространстве приобретает вид

Элементы матрицы 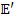представляют собой алгебраическую сумму э.д.с., действующих в контурах. Элементы главной диагонали 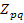представляют собой собственные сопротивления контуров, а остальные элементы этой матрицы являются сопротивлениями связи между контурами. Каждый элемент матрицы — это сумма разностей потенциалов между зажимами элементов ветвей, встречаемых при последовательном обходе контура. Из 2-го закона Кирхгофа эта сумма равна нулю.

Отсюда

(в ранее приведенных обозначениях это соответствует ). Таким образом, соотношение значительно упрощается в пространстве и становиться системой из уравнений с искомыми неизвестными:

.

В основе эквивалентных преобразований электрических цепей в диакоптике лежит постулат инвариантности мощности

.

Последовательность решения задачи методом диакоптики для чистоконтурной цепи (рис.22 а), т.е. цепи, содержащей число контуров равное числу элементарных двухполюсных ветвей, такова.

1. Устанавливают примитивную контурную цепь. Например разделив исходную цепь на короткозамкнутых частей с токами короткого замыкания, равными токам исходной ветви и приложенными э.д.с. (рис.22 б).

2. Устанавливают тензор полного сопротивления примитивной цепи с числом строк и столбцов, равных числу элементов примитивной цепи.

3. Записывают вектора r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>»> 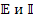примитивной цепи.

4. Получают матрицу преобразований .

5. Определяют новые компоненты тензора полного сопротивления

6.

Тензорное исчисление для чайников

Записывают контурные напряжения и уравнение напряжения новой цепи .

7. Производят обращение тензора полного сопротивления новой цепи

8. Находят неизвестные токи и напряжения .

Разумеется для простых цепей применение диакоптики не оправдано, однако, по мере усложнения цепи и наличия в ней отдельных идентичных элементарных цепей при большом числе электромагнитных связей, затраты умственного и физического труда с применением диакоптики сокращаются пропорционально сложности цепи. Кроме того, применение диакоптики позволяет активно использовать машинные методы расчета.

 

1234

ПОСМОТРЕТЬ ЕЩЕ: