Слово рекурсия

Слово рекурсия английскими буквами(транслитом) — rekursiya

Слово рекурсия состоит из 8 букв: е и к р р с у я

---

Значения слова рекурсия. Что такое рекурсия?

Рекурсия

Реку́рсия — наличие в определении, описании, изображении какого-либо объекта или процесса самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя.

ru.wikipedia.org

Рекурсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса или метода…

Энциклопедический фонд России

РЕКУРСИЯ — способ определения функций, являющийся объектом изучения в теории алгоритмов и других разделах математич. логики. Этот способ давно применяется в арифметике для определения числовых последовательностей (прогрессии, чисел Фибоначчи и пр.).

Математическая энциклопедия. — 1977-1985

Рекурсия (фонетика)

Рекурсия в фонетике — конечный этап артикуляции. Известно, что в звучащей речи фонемы произносятся не одна за другой, а слитно. Речевой аппарат добивается этого за счёт подгонки рекурсии предыдущего звука под экскурсию последующего.

ru.wikipedia.org

Хвостовая рекурсия

Хвостовая рекурсия — специальный случай рекурсии, при котором рекурсивный вызов функцией самой себя является её последней операцией. Подобный вид рекурсии примечателен тем, что может быть легко заменён на итерацию…

ru.wikipedia.org

ПРИМИТИВНАЯ РЕКУРСИЯ

ПРИМИТИВНАЯ РЕКУРСИЯ — способ определения функций от натуральных аргументов с натуральными значениями. Говорят, что (n+1)-местная функция f(x 1, …, х п, у). получена примитивной рекурсией из n-местной функции g…

Математическая энциклопедия. — 1977-1985

МНОГОКРАТНАЯ РЕКУРСИЯ

МНОГОКРАТНАЯ РЕКУРСИЯ — вид рекурсии, в к-рой участвуют сразу несколько переменных. Наборы значений этих переменных упорядочиваются лексикографически. Под это определение подходят многочисленные конкретные рекурсивные описания.

Математическая энциклопедия. — 1977-1985

РЕКУРСИИ ВЫСШИХ СТУПЕНЕЙ

РЕКУРСИИ ВЫСШИХ СТУПЕНЕЙ — рекурсивные определения, в к-рых в качестве вспомогательных объектов наряду с числовыми функциями используются нек-рые функционалы более высоких типов.

Математическая энциклопедия. — 1977-1985

Рекурсивная функция (теория вычислимости)

Термин рекурсивная функция в теории вычислимости используется для обозначения трёх классов функций примитивно рекурсивные функции; общерекурсивные функции; частично рекурсивные функции. Последние совпадают с классом вычислимых по Тьюрингу функций.Оно состоит из указания класса базовых примитивно рекурсивных функций и двух операторов (суперпозиции и примитивной рекурсии), позволяющих строить новые примитивно рекурсивные функции на…

ru.wikipedia.org

Рекурсивные функции (от позднелатинского recursio — возвращение), название, закрепившееся за одним из наиболее распространённых вариантов уточнения общего понятия арифметического алгоритма, т.е. такого алгоритма…Оператор примитивной рекурсии сопоставляет функциям f от n переменных и g от n + 2 переменных функцию h от n + 1 переменных такую, что для любых натуральных чисел x1,…., xn, y h(x1…

БСЭ. — 1969—1978

РЕКУРСИВНАЯ ФУНКЦИЯ — ч а с т и ч н о р е к у р с и в н а я ф у н к ц и я,- одно из математич. уточнений интуитивного понятия вычислимой функции, определяемое следующим образом….f наз. р е к у р с и в н о й, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и минимизации..

Математическая энциклопедия. — 1977-1985

---

Рекурсивные функции

а) Терминологическое введение

По сути один и тот же метод, применительно к различным областям носит различные названия – это индукция, рекурсия и рекуррентные соотношения – различия касаются особенностей использования.

Под индукцией понимается метод доказательства утверждений, который строится на базе индукции при n=0,1, затем утверждение полагается правильным при n=n b и проводится доказательство для n+1.

Под рекурсией понимается метод определения функции через её предыдущие и ранее определенные значения, а так же способ организации вычислений, при котором функция вызывает сама себя с другим аргументом.

Термин рекуррентные соотношения связан с американским научным стилем и определяет математическое задание функции с помощью рекурсии.

Основной задачей исследования рекурсивно заданных функций является получение f(n) в явной или как еще говорят «замкнутой» форме, т.е. в виде аналитически заданной функции. В связи с этим рассмотрим ряд примеров:

б) Примеры рекурсивного задания функций

1.

f(0)=0 f(n)= f(n-1)+1

2.

f(0)=1 f(n)= n*f(n-1)

Последовательная подстановка дает – f(n)=1*2*3*…*n = n!

Для полноты сведений приведем формулу Стирлинга для приближенного вычисления факториала для больших n: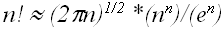

3.

f(0)=1 f(1)=1 f(n)= f(n-1)+ f(n-2), n>=2

Эта рекурсивная функция определяет числа Фибоначчи: 1 1 2 3 5 8 13, которые достаточно часто возникают при анализе различных задач, в том числе и при анализе алгоритмов. Отметим, что асимптотически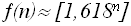

4.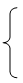

f(0)=1 f(n)= f(n-1)+ f(n-2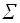)+…+1 = f(i)+1

Для получения функции в явном виде рассмотрим ее последовательные значения: f(0)=1, f(1)=2, f(2)=4, f(3)=8, что позволяет предположить, что f(n)=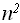, точное доказательство выполняется по индукции.

5.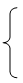

f(0)=1 f(n)= 2*f(n-1)

Мы имеем дело с примером того, что одна и та же функция может иметь различные рекурсивные определения – f(n)=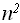, как и в примере 4, что проверяется элементарной подстановкой.

6.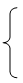

f(0)=1 f(1)=2 f(n)= f(n-1)*f(n-2)

В этом случае мы можем получить решение в замкнутой форме, сопоставив значениям функции соответствующие степени двойки:

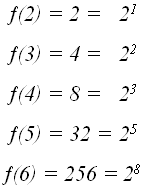
Обозначив через Fn — n-ое число Фибоначчи, имеем: f(n)=.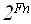

Рекурсивная реализация алгоритмов

Большинство современных языков высокого уровня поддерживают механизм рекурсивного вызова, когда функция, как элемент структуры языка программирования, возвращающая вычисленное значение по своему имени, может вызывать сама себя с другим аргументом.

Рекурсия в программировании

Эта возможность позволяет напрямую реализовывать вычисление рекурсивно определенных функций. Отметим, что в силу тезиса Черча–Тьюринга аппарат рекурсивных функций Черча равномощен машине Тьюринга, и, следовательно, любой рекурсивный алгоритм может быть реализован итерационно.

F(n);
If n=0 or n=1 (проверка возможности прямого вычисления)
Then
F <— 1
Else
F <— n*F(n-1); ( рекурсивный вызов функции)
Return (F);
End;

Анализ трудоемкости рекурсивных реализаций алгоритмов, очевидно, связан как с количеством операций, выполняемых при одном вызове функции, так и с количеством таких вызовов. Графическое представление порождаемой данным алгоритмом цепочки рекурсивных вызовов называется деревом рекурсивных вызовов. Более детальное рассмотрение приводит к необходимости учета затрат как на организацию вызова функции и передачи параметров, так и на возврат вычисленных значений и передачу управления в точку вызова.

Можно заметить, что некоторая ветвь дерева рекурсивных вызовов обрывается при достижении такого значения передаваемого параметра, при котором функция может быть вычислена непосредственно. Таким образом, рекурсия эквивалентна конструкции цикла, в котором каждый проход есть выполнение рекурсивной функции с заданным параметром.

Рассмотрим пример для функции вычисления факториала (рис 8.1):

Цепочка рекурсивных возвратов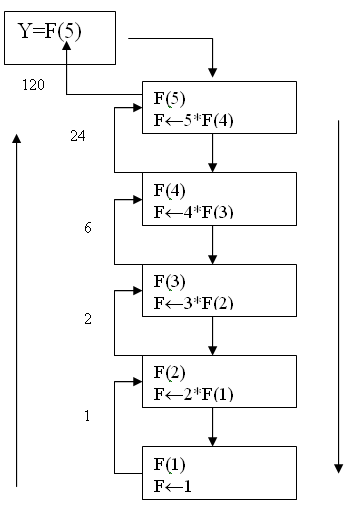

Цепочка рекурсивных вызовов

Рис 8.1 Дерево рекурсии при вычислении факториала – F(5)

Дерево рекурсивных вызовов может иметь и более сложную структуру, если на каждом вызове порождается несколько обращений – фрагмент дерева рекурсий для чисел Фибоначчи представлен на рис 8.2:

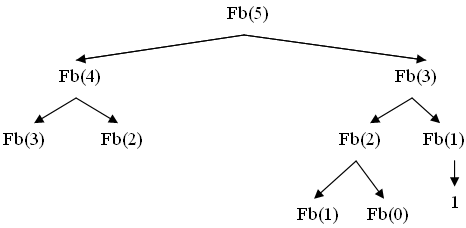
Рис 8.2 Фрагмент дерева рекурсии при вычислении чисел Фибоначчи – F(5)

Анализ трудоемкости механизма вызова процедуры

Механизм вызова функции или процедуры в языке высокого уровня существенно зависит от архитектуры компьютера и операционной системы. В рамках IBM PC совместимых компьютеров этот механизм реализован через программный стек. Как передаваемые в процедуру или функцию фактические параметры, так и возвращаемые из них значения помещаются в программный стек специальными командами процессора. Дополнительно сохраняются зна-чения необходимых регистров и адрес возврата в вызывающую процедуру. Схематично этот механизм иллюстрирован на рис 8.3:

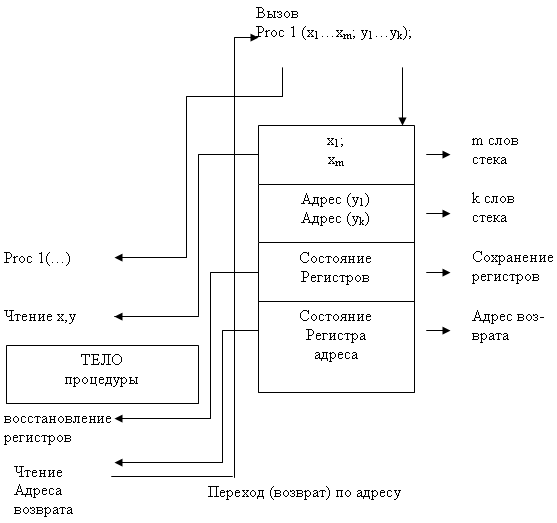
Рис 8.2 Механизм вызова процедуры с использованием программного стека

Для подсчета трудоемкости вызова будем считать операции помещения слова в стек и выталкивания из стека элементарными операциями в формальной системе. Тогда при вызове процедуры или функции в стек помещается адрес возврата, состояние необходимых регистров процессора, адреса возвращаемых значений и передаваемые параметры. После этого выполняется переход по адресу на вызываемую процедуру, которая извлекает переданные фактические параметры, выполняет вычисления, помещает их по указанным в стеке адресам, и при завершении работы восстанавливает регистры, выталкивает из стека адрес возврата и осуществляет переход по этому адресу.

Обозначив через:
m — количество передаваемых фактических параметров,
k — количество возвращаемых процедурой значений,
r — количество сохраняемых в стеке регистров,
имеем:

fвызова = m+k+r+1+m+k+r+1 = 2*(m+k+r+1) элементарных операций на один вызов и возврат.

Анализ трудоемкости рекурсивных алгоритмов в части трудоемкости самого рекурсивного вызова можно выполнять разными способами в зависимости от того, как формируется итоговая сумма элементарных операций – рассмотрением в отдельности цепочки рекурсивных вызовов и возвратов, или совокупно по вершинам дерева рекурсивных вызовов.

Анализ трудоемкости алгоритма вычисления факториала

Для рассмотренного выше рекурсивного алгоритма вычисления факториала количество вершин рекурсивного дерева равно, очевидно, n, при этом передается и возвращается по одному значению (m=1, k=1), в предположении о сохранении четырех регистров – r=4, а на последнем рекурсивном вызове значение функции вычисляется непосредственно – в итоге:

fa(n)=n*2*(1+1+4+1)+(n-1)*(1+3)+1*2=18*n — 2

Отметим, что n – параметр алгоритма, а не количество слов на входе.

Информатика и программирование

Рекурсия

Рис. 16.2. Вычисление функции Factorial(n) для n=4.

Сначала образуется так называемый рекурсивный фрейм №1 при n=4. Для этого фрейма отводится память и в нем фиксируются все значения переменных тела функции при n=4. Отметим, что в рекурсивном фрейме фиксируются значения всех переменных функции, кроме глобальных.

Затем происходит вызов Factorial(n) при n=3. Образуется фрейм №2, где фиксируются значения переменных тела функции при n=3. При этом фрейм №1 также хранится в памяти. Из фрейма №2 происходит обращение к Factorial(n) при n=2. В результате этого обращения образуется фрейм №3, где фиксируются значения переменных тела функции при n=2 и т.д. до тех пор, пока при очередном обращении к функции Factorial условие n>0 не примет значение false.

Это произойдет в фрейме №5. В этом фрейме мы получим значение Factorial =1 и передадим это значение в фрейм №4. После этого фрейм №5 будет уничтожен, так как обращение Factorial(n) при n=0 будет выполнено.

В фрейме №4 мы вычислим значение Factorial(n) для n=1. После чего мы передадим это значение во фрейм №3, а фрейм №4 будет закрыт, так как обращение к Factorial(n) при n=1 будет закончено.

Так мы будем сворачивать эту цепочку фреймов в последовательности, обратной той, в которой мы их порождали, пока не свернем фрейм №1. После чего вычисление функции будет окончено.

Рекурсия возможна не только в случае функций, но и процедур. Пример рекурсии для процедур приведен на рисунке 16.3.

Там показано описание рекурсивной процедуры для распечатки (вывода на печать) строки символов в порядке, обратном их вводу.

Procedure BackPrint ;

var символ : char ;

begin read (символ) ;

if символ = EOL {EOL — EndOfLine — специальное значение типа

СHAR, соответствующее окончанию ввода}

thenwriteln ( ) ; {пред началом вывода надо убедиться, что

печатать будем с новой строки}

else begin BackPrint ; write (символ) end

end {Procedure}

Рис 16.3. Пример рекурсивной процедуры.

(Косвенная рекурсия.) Итерация и рекурсия.

Нетрудно заметить сходство между циклическими конструкциями (повторениями) и рекурсией. На рисунке 16.4 показана схема цикла вида whiledo и его рекурсивного аналога.

Рис. 16.4. Схема организации цикла вида whiledo

и его рекурсивного эквивалента.

Обратите внимание, что в правой части рис. 16.4 возможно зацикливание! Надо быть очень осторожным и всякий раз, применяя рекурсивную поцедуру или функцию, убедиться в их корректном завершении. Рассмотрим пример. На рисунке 16.5 приведен алгоритм Евклида, с которым мы познакомились на лекции 1, для вычисления НОД (наибольшего общего делителя) в форме обычной и рекурсивной функции на языке Pascal.

Function НОД (a, b : integer) : integer ;

Рис. 16.5. Циклическая и рекурсивная функции

для вычисления НОД.

Как видно из приведенных примеров на рисунках 16.1 и 16.5, итерация, т.е. цикл всегда может быть заменен его рекурсивным аналогом по схеме, показанной на рисунке 16.4.

С обратным утверждением о замене рекурсии итерацией все сложнее. На рисунке 16.6 приведен пример рекурсивной функции, где по схеме (рис. 16.4) рекурсию итерацией заменить не удается.

в остальных случаях

Рис. 16.6. Рекурсивная функция Аккермана.

Способы повторного использования процедур и функций.

Итак, процесс абстракции в форме процедуры состоит из трех шагов:

Именование. Присвоить рутинному алгоритму уникальное имя, которое затем будем использовать как имя соответствующей процедуры.

Определить пред- и постусловия для создаваемой процедуры или функции в соответствии с контекстом их использования в основной программе.

Параметризиовать процедуру. (Везде далее, если явно не оговорено, говоря о процедурах, будем иметь в виду также и функции). Для этого часть предусловия и постусловия в спецификации оформить в виде параметров соответствующего типа, часть из которых будет доставлять исходные данные, а другая часть — результаты работы процедуры.

Обобщить типы параметров. Проанализировать все места в программе, где будет обращение к данной процедуре на предмет, какие типы данных используются в этих местах, как они соотносятся с типами параметров в процедуре. Назовем совокупность типов данных в месте вызова процедуры контекстом обращения к процедуре Определить типы параметров так, чтобы они соответствовали как можно большему числу контекстов обращений к процедуре.

Реализовать получившуюся абстракцию рутинного алгоритма либо в форме процедуры, либо функции.

Мы не в праве ожидать, что выделенные нами уже существующие функции или процедуры, которые могут быть нам полезны для создания нашей новой программы, мы сможем использовать в том виде, как они есть. Есть четыре основных способа адаптации или повторного использования уже существующих рутинных алгоритмов и процедур для новых целей. Это — присоединение, вложение, настройка и слияние.

Присоединение. Этот способ предполагает, что если у нас есть процедура P₁ c предусловием Q₁ и постусловием R₁ и процедура P₂ c пред-и c постусловиями Q₂ и R₂ соответственно, (причем R₁ ÞQ₂ ) , то мы можем построить процедуру Pc предусловием Q₁ и постусловием R₂ последовательно соеденив Р₁ и P₂ так, как показано на рис.16.7.

P {Q₁ }

{R₁ ÞQ₂ }

{R₂ }

Рис.

16.7. Присоединение процедур Р₁ и P₂ .

Вложение. Этот способ применяется, когда новая процедура P образуется вложением известной процедуры P₂ внутрь другой известной процедуры P₁ . Вложение возникает либо когда мы явно вставляем P₂ как тело цикла или как альтернативу в теле процедуры P₁ , либо когда P₂ — это параметр для P₁ .

Настройка. Суть этого способа состоит в том, что существующую процедуру Р₁ мы либо обобщаем, либо, наоборот, сужаем в соответствии со спецификацией Р.

Например, если у нас есть процедура выбора максимального числа из массива из 100 натуральных чисел, то легко ее можем обобщить на случай массива из 1000 целочисленных компонентов.

Слияние.

Этот способ построения новой процедуры Р за счет слияния, объединения двух существующих процедур Р₁ и P₂ .

Например, пусть процедура Р₁ выбирает максимальное, а P₂ — минимальное значения в массиве из 100 целых чисел. Тогда, объединив операторы процедуры Р₁ и процедуры P₂ в надлежащем порядке, мы получим процедуру Р , выбирающую max и min из 100 целых чисел.

Рекурсия и итерация.

Рекурсия— это определение понятия самого через себя.

Например, идентификатор ::= <буква>|<идентификатор><буква> |<идентификатор><цифра>

В случае процедур и функций рекурсия используется в виде вызова функции самой себя в собственном теле. Это делается обычно для последовательного понижения размерности (сложности) задачи, пока решение задачи не станет тривиальным (простым). Запись решения задачи в виде последовательности рекурсивных вызовов функции обычно выглядит более понятно (более просто) по сравнении с обычным (нерекурсивным ) (итерационным) решением.

Например, одно и то же вычисление факториала можно сделать несколькими способами:

Нерекурсивное (итерационное) решение:

fact(n) =1*2*3*4*…*n =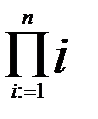

Рекурсивное решение имеет вид:

1, при n=0

Понижение размерности задачи

fact(n) =

fact(n-1)*n при n >0.

4!=(3!)*4

Примеры итерационных вычислений, например, при вычислении значений многоместных (n-арных) операций уже рассматривались выше (когда роль идет о вычислении n – арных операций)

Вычисление с помощью итерации: Рекурсивное определение той же функции:

Предопределенная

константа

Type type

natural=0.. maxint; natural=0.. maxint;

function fact(n: natural): Longint; function fact(n: natural): Longint;

var begin

i: integer; if n = 0 then

f: Longint; fact := 1;

begin else fact := n * fact(n-1); end;

f:= 1; end.

for i:= 1 to n do вычисление значения этого

f:= f * i; выражения будет производиться

fact := f; на рекурсивном возврате (после

end; рекурсивного вызова)

переменная где формируется

результат функции

Процесс рекурсивного вычисления значения в данном случае факториала организуется в соответствии с данным определением. Этот процесс сводится к последовательному вызову функции самой себя каждый раз с новым значением аргумента (цепочке рекурсивных вызовов). При этом каждый раз при каждом таком рекурсивном вызове в стеке откладывается копии всех локальных параметров процедуры или функции:

Fact(3) à 3*Fact(2) à 3*( 2* Fact(1) ) à 3*( 2*( 1* Fact(0)))

Нерекурсивный вызов Fact(0)=1 завершает цепочку рекурсивных вызовов.

В общем случае при вызове любой процедуры или функции происходят следующие действия:

1).

В стеке сохраняются значения локальных объектов подпрограммы (фактические параметры и локальные для вызываемой подпрограммы переменные);

2). Запоминается адрес возврата в вызывающую подпрограмму (или программу);

3). Управление передается вызванной подпрограмме.

В некоторый момент выполнения программы в стеке может присутствовать несколько (возможно даже одинаковых) групп локальных объектов, соответствующих цепочке вызванных, но не завершенных подпрограмм. В каждый момент времени доступ возможен только к той группе, которая включена в стек последней и находится в голове стека. Эта группа локальных объектов соответствует текущей вызванной подпрограмме. Таким образом, в случае, если в стеке оказывается одновременно несколько одноименных переменных, то доступна их будет лишь та, которая попала в стек последней. При завершении вызванной подпрограммы ее локальные объекты удаляются из вершины стека, и в голове стека оказываются (и становятся доступными) локальные объекты вызывающей подпрограммы.

Рассмотрим процесс рекурсивного определения более подробно на примере вызова y:=fact(3).

Fact(3) Первичный вызов n 3

Fact ? 6

Fact(2) n 2 fact(2)*3

спуск рекурсивные вызовы Fact ? 2 возврат

Fact(1) n 1 fact(1)*2

Fact ? 1

Fact(0) n 0 fact(0)*1

содержимое стекаFact 1

имя

значения имя при рекурсивных вызовах

вычисляемые значения при рекурсивных возвратах

Такой процесс последовательного вызова функции самой себя естественно с разными значениями аргумента называется рекурсивным спуском. В процессе рекурсивного спуска при каждом рекурсивном вызове в стеке выделяется память под копию каждого локального параметра. Процесс рекурсивного спуска будет продолжаться до тех пор, пока выражение в правой части оператора присваивания для вычисления возвращаемого значения не примет вполне определенный вид (в этом случае функция сама себя не вызывает). В данном случае конец наступит, когда при очередном рекурсивном вызове аргумент будет равен 0, после этого процесс начнет раскручиваться в обратную сторону — будет происходить рекурсивный возврат. Этот процесс сопровождается освобождением памяти(в стеке), занимаемой очередной копией локальных объектов процедур или функций.

Действия в теле рекурсивных процедур и функций могут выполняться либо на рекурсивном спуске (до рекурсивного вызова) , либо на рекурсивном возврате (после рекурсивного вызова). В данном случае действие (вычисление факториала) происходит в процессе рекурсивного возврата и имеет следующий вид:

то, что получено после рекурсивного вызова

fact(n) = fact(n-1) * n.

Количество вызовов функцией самой себя при рекурсивном спуске называется глубинойрекурсии.

Необходимыми условиями для успешного завершения рекурсии процедур или функций являются следующие:

1). необходимо точно определить ситуацию, при которой должен завершиться рекурсивный спуск. В данном случае такая ситуация имеет вид: n =0 — один признак у этой ситуации Но может быть и более сложный случай.

2) необходимо предусмотреть в теле рекурсивной подпрограммы тех действий, которые должны приближать наступление указанной выше ситуации.

Каждую рекурсию можно заменить итерацией, применив цикл. Рекурсивное определение алгоритма обычно более просто и компактно. Можно считать, что при рекурсивном определении говорится, что нужно сделать, но не говорится как. При итерационном наоборот: строго формулируется, что и как нужно сделать.

У рекурсивной процедуры или функции имеются следующие недостатки: на выполнение рекурсии процедуры или функции требуется большое количество машинного времени и памяти.

Времени требуется больше потому, что многократно вызываются процедуры и функции, т.е. тратиться время на то, чтобы выйти и войти в нее. Память тратится больше из-за того что при каждом рекурсивном вызове резервируется память в стеке для каждого локального объекта процедуры или функции. Для контроля переполнения стека используется директива {$S+}. Для сокращения памяти в стеке (при этом увеличатся затраты памяти в сегменте данных) при рекурсивном вызове (при предполагаемом большом числе рекурсивных вызовов), целесообразно использовать статические локальные переменные — на Паскале это типизированные константы (память под них выделяется не в стеке, а сегменте данных).

Не каждый алгоритм может быть успешно реализован с помощью рекурсии. Успешно алгоритм может быть реализован, если удалось определить ситуацию, при наступлении которой завершится процесс рекурсивного спуска.

Похожие статьи:

Если вкратце, то:
grep -rn word /directory

Теперь подробнее. Что такое grep, вы, скорее всего, уже знаете. Эта утилита используется как фильтр вывода текстовой информации в консоли.

-r — grep обойдёт каталог рекурсивно

-n — grep выведет номер строки в результатах

word — указываем слово, которое ищем

/directory — указываем директорию.

Например /home/$user/docs

Несколько примеров.

inky@support68:~$ grep -rn word /home/inky/docs/
/home/inky/docs/doc1.txt:11:some word here
В 11й строке файла /home/inky/docs/doc1.txt содержится слово word (после 11: выводится сама строка)

inky@support68:~$ grep -rn «few words» /home/inky/docs/
/home/inky/docs/doc1.txt:19:few words here
В 19й строке файла нашлось словосочетание few words.

Ну и пример с egrep:
inky@support68:~$ egrep -rn ‘(word1|word2|word3)’ /home/inky/docs/
/home/inky/docs/doc1.txt:20:word1
/home/inky/docs/doc1.txt:21:word2
/home/inky/docs/doc1.txt:22:word3
Мы искали word1 или word2 или word3. В 20й строчке нашлось word1, в 21й — word2, в 22й — word3.

Использую я это в основном для поиска iframe на хостинг-серверах. Иногда полезно также найти что-либо в каталогах с большим количеством конфигурационных файлов.
Enjoy =)

Тренировочные задачи на рекурсию

В этом листке собраны тренировочные задачи. Их решение необязательно, но рекомендуется тем, кто плохо освоил задачи на рекурсию. Также в этом листке есть несколько довольно сложных задач, которые могут быть интересны всем. Задачи из этого листка не учитываются при выставлении оценок.

Задачи можно сдавать на языках C++ и Python, поэтому если вы хотите попрактиковаться в другом языке, то тоже можете сдавать задачи.

В задачах этого листка нельзя использовать циклы и массивы. Также могут быть и другие ограничения в каких-то конкретных задачах (например, запрет использования строк в арифметических задачах, запрет использования срезов в решениях на питоне).

Задачи проверяются только автоматически и сразу же получают OK при прохождении всех тестов. Однако, если при последующей проверке кода будет выявлено нарушение вышеизложенных требований или будут другие замечания к решению, статус OK может быть изменен.

A: От 1 до n

Дано натуральное число \(n\). Выведите все числа от 1 до \(n\).

B: От A до B

Даны два целых числа A и В (каждое в отдельной строке). Выведите все числа от A до B включительно, в порядке возрастания, если , или в порядке убывания в противном случае.

C: Функция Аккермана

В теории вычислимости важную роль играет функция Аккермана \(A(m, n)\), определенная следующим образом: \[ A(m, n) = \begin{cases} n + 1 & m = 0\\ A(m — 1, 1)& m > 0, n = 0\\ A(m — 1, A(m, n — 1))& m > 0, n > 0\\ \end{cases} \]

Даны два целых неотрицательных числа \(m\) и \(n\), каждое в отдельной строке. Выведите \(A(m, n)\).

D: Точная степень двойки

Дано натуральное число N. Выведите слово , если число N является точной степенью двойки, или слово в противном случае.

Операцией возведения в степень пользоваться нельзя!

E: Сумма цифр числа

Дано натуральное число N. Вычислите сумму его цифр.

При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется).

F: Цифры числа справа налево

Дано натуральное число N. Выведите все его цифры по одной, в обратном порядке, разделяя их пробелами или новыми строками.

При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.

G: Цифры числа слева направо

Дано натуральное число N. Выведите все его цифры по одной, в обычном порядке, разделяя их пробелами или новыми строками.

При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.

H: Проверка числа на простоту

Дано натуральное число \(n>1\). Проверьте, является ли оно простым. Программа должна вывести слово , если число простое и , если число составное. Алгоритм должен иметь сложность \(O(\sqrt{n})\).

Указание. Понятно, что задача сама по себе нерекурсивна, т.к. проверка числа \(n\) на простоту никак не сводится к проверке на простоту меньших чисел. Поэтому нужно сделать еще один параметр рекурсии: делитель числа, и именно по этому параметру и делать рекурсию.

I: Разложение на множители

Дано натуральное число \(n>1\). Выведите все простые делители этого числа в порядке неубывания с учетом кратности. Алгоритм должен иметь сложность \(O(\sqrt{n})\).

J: Палиндром

Дано слово, состоящее только из строчных латинских букв. Проверьте, является ли это слово палиндромом. Выведите или .

При решении этой задачи нельзя пользоваться циклами, в решениях на питоне нельзя использовать срезы с шагом, отличным от 1.

Ввод	Вывод
radar	YES
yes	NO

K: Вывести нечетные числа последовательности

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите все нечетные числа из этой последовательности, сохраняя их порядок.

В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.

L: Вывести члены последовательности с нечетными номерами

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите первое, третье, пятое и т.д. из введенных чисел. Завершающий ноль выводить не надо.

В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.

M: Максимум последовательности

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите наибольшее значение числа в этой последовательности.

В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция возвращает единственное значение: максимум считанной последовательности. Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).

N: Среднее значение последовательности

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите среднее значение элементов этой последовательности (без учета последнего нуля).

В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает кортеж из пары чисел: число элементов в последовательности и их сумма. В программе на языке C++ результат записывается в две переменные, которые передаются в функцию по ссылке.

Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).

Ввод	Вывод
1 7 9 0	5.666666666666667

O: Второй максимум

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите значение второго по величине элемента в этой последовательности, то есть элемента, который будет наибольшим, если из последовательности удалить наибольший элемент.

В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.

Гарантируется, что последовательность содержит хотя бы два числа (кроме нуля).

Ввод	Вывод
1 7 9 0	7
1 2 2 1 0	2

P: Количество элементов, равных максимуму

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите, какое количество элементов этой последовательности, равны ее наибольшему элементу.

В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра.

В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.

Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).

Ввод	Вывод
1 7 9 0	1
1 3 3 1 0	2

Q: Количество единиц

Дана последовательность натуральных чисел (одно число в строке), завершающаяся двумя числами 0 подряд. Определите, сколько раз в этой последовательности встречается число 1. Числа, идущие после двух нулей, необходимо игнорировать.

В этой задаче нельзя использовать глобальные переменные и параметры, передаваемые в функцию. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметров.

R: Треугольная последовательность

Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, …

По данному натуральному n выведите первые n членов этой последовательности. Попробуйте обойтись только одним циклом for.

Ввод	Вывод
2	1 2
5	1 2 2 3 3

S: Заданная сумма цифр

Даны натуральные числа \(k\) и \(s\). Определите, сколько существует \(k\)-значных натуральных чисел, сумма цифр которых равна \(d\). Запись натурального числа не может начинаться с цифры 0.

В этой задаче можно использовать цикл для перебора всех цифр, стоящих на какой-либо позиции.

T: Без двух нулей

Даны числа \(a\) и \(b\). Определите, сколько существует последовательностей из \(a\) нулей и \(b\) единиц, в которых никакие два нуля не стоят рядом.

U: Разворот числа

Дано число \(n\), десятичная запись которого не содержит нулей. Получите число, записанное теми же цифрами, но в противоположном порядке.

При решении этой задачи нельзя использовать циклы, строки, списки, массивы, разрешается только рекурсия и целочисленная арифметика.

Фунция должна возвращать целое число, являющееся результатом работы программы, выводить число по одной цифре нельзя.