admin / 02.12.2017
1. Основные этапы развития топологии
.
Содержание
Топология
От древнегреческих слов τόπος — место и λόγος — слово, учение происходит математический термин топология. Топология — раздел геометрии, предметом изучения которого является явление непрырывности, в частности, свойства пространства, к примеру, связность, ориентируемость, которые остаются неизменными при непрерывных деформациях.
Зародилась топология на рубеже XIX-XX веков. Первые работы по топологии были написаны Эйлером, Жорданом, Кантором и Пуанкаре.
Сетевая топология
Первое время топологию называли геометрией размещения или анализом размещения. Начиная с 1925 по 1975 годы, топология являлась одним из важнейших направлений развития математической науки. В самостоятельную математическую науку топология превратилась в середине XX в. Основные постулаты топологии были заложены в работах таких известных ученых, как Хаусдорф, Пуанкаре, Александров, Урысон, Брауэр.
В отличие от геометрии, топология не рассматривает метрические свойства объектов. Таким образом, с точки зрения топологии круг и бублик неотличимы.
Для топологии очень важны понятия геоморфизма и гомотопии. В широком смысле эти понятия обозначают разного рода деформации, происходящие без разрывов и склеиваний. В более узком смысле топологией или топологической структурой называется конкретный объект как совокупность всех открытых множеств, использующихся в определении топологического пространства.
Таким образом, топология объекта — это то, что остается неизменным при непрерывных деформациях.
К основным разделам топологии относятся:
- Общая топология или теоретико-множественная топология — раздел топологии, изучающий непрерывности в чистом виде, занимающийся исследованием фундаментальных вопросов топологии, к примеру связность и компактность.
- Алгебраическая топология — раздел, изучающий непрерывности алгебраических объектов типа гомотопических групп и гомологии.
- Дифференциальная топология — раздел топологии, в котором изучаются гладкие многообразия с точностью до диффеоморфизма, а также из включения в другие многообразия. Дифференциальная топология имеет два подраздела: маломерная топология и теория узлов.
Поделиться ссылкой

Лента Мёбиуса — поверхность с одной стороной и одним краем; пример объекта, изучаемого в топологии
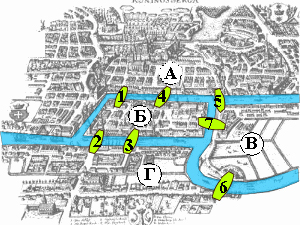
Семь мостов Кёнигсберга — одна из первых задач топологии, рассмотренная Эйлером.
Материал из ПИЭ.Wiki
Перейти к: навигация, поиск
Термин «топология», или «топология сети», характеризует физическое расположение компьютеров, кабелей и других компонентов сети.
Топология — это стандартный термин, который используется профессионалами при описании основной компоновки сети.
Сетевая топология — способ описания конфигурации сети, схема расположения и соединения сетевых устройств.
Сетевая топология может быть
• физической — описывает реальное расположение и связи между узлами сети.
• логической — описывает хождение сигнала в рамках физической топологии.
Базовые топологии
Все сети строятся на основе трех базовых топологий:
• шина (bus);
• звезда (star);
• кольцо (ring).
Остальные способы являются комбинациями базовых. В общем случае такие топологии называются смешанными или гибридными, но некоторые из них имеют собственные названия, например «Дерево».
Каждая топология сети налагает ряд условий. Например, она может диктовать не только тип кабеля, но и способ его прокладки. Топология может также определять способ взаимодействия компьютеров в сети. Различным видам топологий соответствуют различные методы взаимодействия, и эти методы оказывают большое влияние на сеть.
Шина
Топологию «шина» часто называют «линейной шиной» (linear bus). Данная топология относится к наиболее простым и широко распространенным топологиям. В ней используется один кабель, именуемый магистралью или сегментом, вдоль которого подключены все компьютеры сети.

Рис. 1.1. Сетевая топология «шина»
Взаимодействие компьютеров
В сети с топологией «шина» компьютеры адресуют данные конкретному компьютеру, передавая их по кабелю в виде электрических сигналов. Однако через особенности распространения электрических сигналов по длинным линиям связи необходимо предусматривать включение на концах шины специальных устройств – терминаторов. Без включения терминаторов сигнал отражается от конца линии и искажается так, что связь по сети становится невозможной.
Передача сигнала
Данные в виде электрических сигналов передаются всем компьютерам сети; однако информацию принимает только тот, адрес которого соответствует адресу получателя, зашифрованному в этих сигналах.
1. Основные этапы развития топологии
Причем в каждый момент времени только один компьютер может вести передачу.
Так как данные в сеть передаются лишь одним компьютером, ее производительность зависит от количества компьютеров, подключенных к шине. Чем их больше, т.е. чем больше компьютеров, ожидающих передачи данных, тем медленнее сеть. Однако вывести прямую зависимость между пропускной способностью сети и количеством компьютеров в ней нельзя. Ибо, кроме числа компьютеров, на быстродействие сети влияет множество факторов, в том числе:
• характеристики аппаратного обеспечения компьютеров в сети;
• частота, с которой компьютеры передают данные;
• тип работающих сетевых приложений;
• тип сетевого кабеля;
• расстояние между компьютерами в сети.
Шина — пассивная топология. Это значит, что компьютеры только «слушают» передаваемые по сети данные, но не перемещают их от отправителя к получателю. Поэтому, если один из компьютеров выйдет из строя, это не скажется на работе остальных. В активных топологиях компьютеры регенерируют сигналы и передают их по сети.
Сравнение с другими топологиями
Достоинства
• Небольшое время установки сети;
• Дешевизна (требуется меньше кабеля и сетевых устройств);
• Простота настройки;
• Выход из строя рабочей станции не отражается на работе сети.
Недостатки
• Любые неполадки в сети, как обрыв кабеля, выход из строя терминатора полностью уничтожают работу всей сети;
• Сложная локализация неисправностей;
• С добавлением новых рабочих станций падает производительность сети.
Звезда
При топологии «звезда» все компьютеры с помощью сегментов кабеля подключаются к центральному компоненту, именуемому концентратором (hub). Сигналы от передающего компьютера поступают через концентратор ко всем остальным. Эта топология возникла на заре вычислительной техники, когда компьютеры были подключены к центральному, главному, компьютеру.

Рис. 1.2. Сетевая топология «звезда»
В сетях с топологией «звезда» подключение кабеля и управление конфигурацией сети централизованны. Но есть и недостаток: так как все компьютеры подключены к центральной точке, для больших сетей значительно увеличивается расход кабеля. К тому же, если центральный компонент выйдет из строя, нарушится работа всей сети. А если выйдет из строя только один компьютер (или кабель, соединяющий его с концентратором), то лишь этот компьютер не сможет передавать или принимать данные по сети. На остальные компьютеры в сети это не повлияет.
Активная звезда
В центре сети содержится компьютер, который выступает в роли сервера.
Пассивная звезда
В центре сети с данной топологией содержится не компьютер, а концентратор, или хаб (hub), что выполняет ту же функцию, что и репитер. Он возобновляет сигналы, которые поступают, и пересылает их в другие линии связи.
Сравнение с другими типами сетей
Достоинства
• выход из строя одной рабочей станции не отражается на работе всей сети в целом;
• хорошая масштабируемость сети;
• лёгкий поиск неисправностей и обрывов в сети;
• высокая производительность сети (при условии правильного проектирования);
• гибкие возможности администрирования.
Недостатки
• выход из строя центрального концентратора обернётся неработоспособностью сети (или сегмента сети) в целом;
• для прокладки сети зачастую требуется больше кабеля, чем для большинства других топологий;
• конечное число рабочих станций в сети (или сегменте сети) ограничено количеством портов в центральном концентраторе.
Кольцо
При топологии «кольцо» компьютеры подключаются к кабелю, замкнутому в кольцо. Сигналы передаются по кольцу в одном направлении и проходят через каждый компьютер. В отличие от пассивной топологии «шина», здесь каждый компьютер выступает в роли репитера, усиливая сигналы и передавая их следующему компьютеру. Поэтому, если выйдет из строя один компьютер, прекращает функционировать вся сеть.

Рис. 1.3. Сетевая топология «кольцо»
Передача маркера
Один из принципов передачи данных в кольцевой сети носит название передачи маркера. Суть его такова. Маркер последовательно, от одного компьютера к другому, передается до тех пор, пока его не получит тот, который «хочет» передать данные. Передающий компьютер изменяет маркер, помещает электронный адрес в данные и посылает их по кольцу. Данные проходят через каждый компьютер, пока не окажутся у того, чей адрес совпадает с адресом получателя, указанным в данных.
После этого принимающий компьютер посылает передающему сообщение, где подтверждает факт приёма данных. Получим подтверждение, передающий компьютер создаёт новый маркер и возвращает его в сеть. На первый взгляд кажется, что передача маркера отнимает много времени, однако на самом деле маркер передвигается практически со скоростью света. В кольце диаметром 200 м маркер может циркулировать с частотой 10 000 оборотов в секунду.
Сравнение с другими топологиями
Достоинства
- Простота установки;
- Практически полное отсутствие дополнительного оборудования;
- Возможность устойчивой работы без существенного падения скорости передачи данных при интенсивной загрузке сети, поскольку использование маркера исключает возможность возникновения коллизий.
Недостатки
- Выход из строя одной рабочей станции, и другие неполадки (обрыв кабеля), отражаются на работоспособности всей сети;
- Сложность конфигурирования и настройки;
- Сложность поиска неисправностей.
Применение
Наиболее широкое применение получила в оптоволоконных сетях. Используется в стандартах FDDI, Token Ring.
Двойное кольцо — это сеть построенная на двух оптоволоконных кольцах, соединяющих компьютеры с двумя сетевыми картами кольцевой топологией. Для повышения отказоустойчивости, сеть строится на оптоволоконных кольцах образующих основной и резервный путь для передачи данных. Первое кольцо используется для передачи данных, а второе не используется. При выходе из строя 1-го кольца оно объединяется со 2-м и сеть продолжает функционировать. Данные при этом по первому кольцу передаются в одном направлении, а по второму в обратном. Используется маркерный метод доступа. Примером может быть сеть двойного кольца FDDI.
Категория: Вычислительные системы, сети и телекоммуникации
Предложенное Эйлером решение задачи о кенигсбергских мостах зависит только от взаимного расположения мостов. Оно положило формальное начало топологии как разделу математики. К.Гаусс (1777–1855) создал теорию узлов, которой позднее занимались И.Листинг (1808–1882), П.Тэйт (1831–1901) и Дж.Александер. В 1840 А.Мёбиус (1790–1868) сформулировал так называемую проблему четырех красок, которую впоследствии исследовали О.де Морган (1806–1871) и А.Кэли (1821–1895). Первым систематическим трудом по топологии были
Предварительные исследования по топологии Листинга (1874).
Основателями современной топологии являются Г.Кантор (1845–1918), А.Пуанкаре (1854–1912) и Л.Брауэр (1881–1966).
Разделы топологии. Топологию можно подразделить на три области: 1) комбинаторную топологию, изучающую геометрические формы посредством их разбиения на простейшие фигуры, регулярным образом примыкающие друг к другу; 2) алгебраическую топологию, занимающуюся изучением алгебраических структур, связанных с топологическими пространствами, с упором на теорию групп; 3) теоретико-множественную топологию, изучающую множества как скопления точек (в отличие от комбинаторных методов, представляющих объект как объединение более простых объектов) и описывающую множества в терминах таких топологических свойств, как открытость, замкнутость, связность и т.д. Разумеется, такое деление топологии на области в чем-то произвольно; многие топологи предпочитают выделять в ней другие разделы. Некоторые основные понятия. Топологическое пространство состоит из множества точек S и набора Sподмножеств множества S, удовлетворяющего следующим аксиомам:
(1) все множество
S и пустое множество принадлежат набору S; (2) объединение любой совокупности множеств из S есть множество из S; (3) пересечение любого конечного числа множеств из S есть множество из S.
Множества, входящие в набор S, называются открытыми множествами, а сам этот набор – топологией в S.Топологическое преобразование, или гомеоморфизм, одной геометрической фигуры S на другую, Sў, – это отображение (p®pў) точек p из Sв точки pўиз Sў, удовлетворяющее следующим условиям: 1) устанавливаемое им соответствие между точками из Sи Sў взаимно однозначно, т.е. каждой точке p из S соответствует только одна точка pў из Sў и в каждую точку pўотображается только одна точка p; 2) отображение взаимно непрерывно (непрерывно в обе стороны), т.е. если заданы две точки p, qиз Sи точка p движется так, что расстояние между ней и точкой q стремится к нулю, то расстояние между соответствующими точками pў, qўиз Sўтакже стремится к нулю, и наоборот.
Геометрические фигуры, переходящие одна в другую при топологических преобразованиях, называются
гомеоморфными. Окружность и граница квадрата гомеоморфны, так как их можно перевести друг в друга топологическим преобразованием (т.е. изгибанием и растяжением без разрывов и склеиваний, например, растяжением границы квадрата на описанную вокруг него окружность). Сфера и поверхность куба также гомеоморфны. Чтобы доказать гомеоморфность фигур, достаточно указать соответствующее преобразование, но тот факт, что для каких-то фигур найти преобразование нам не удается, не доказывает, что эти фигуры не гомеоморфны. Здесь помогают топологические свойства.  Топологическим свойством (или топологическим инвариантом) геометрических фигур называется свойство, которым вместе с данной фигурой обладает также любая фигура, в которую она переходит при топологическом преобразовании.
Топологическим свойством (или топологическим инвариантом) геометрических фигур называется свойство, которым вместе с данной фигурой обладает также любая фигура, в которую она переходит при топологическом преобразовании.
Любое открытое связное множество, содержащее по крайней мере одну точку, называется
областью. Область, в которой любую замкнутую простую (т.е. гомеоморфную окружности) кривую можно стянуть в точку, оставаясь все время в этой области, называется односвязной, а соответствующее свойство области – односвязностью. Если же некоторую замкнутую простую кривую этой области нельзя стянуть в точку, оставаясь все время в этой области, то область называется многосвязной, а соответствующее свойство области – многосвязностью. Представьте себе две круговые области, или диски, одну без дыр, а другую с дырами. Первая область односвязна, вторая многосвязна. Односвязность и многосвязность – топологические свойства. Область с дырой не может перейти при гомеоморфизме в область без дыр. Интересно отметить, что если в многосвязном диске провести по разрезу от каждой из дыр до края диска, то он станет односвязным.
Максимальное число замкнутых простых непересекающихся кривых, по которым можно разрезать замкнутую поверхность, не разделяя ее на отдельные части, называется
родом поверхности. Род – топологический инвариант поверхности. Можно доказать, что род сферы равен нулю, род тора (поверхности «бублика») – единице, род кренделя (тора с двумя дырками) – двум, род поверхности с p дырами равен p. Отсюда следует, что ни поверхность куба, ни сфера не гомеоморфны тору.
Среди топологических инвариантов поверхности можно также отметить число сторон и число краев. Диск имеет 2 стороны, 1 край и род 0. Тор имеет 2 стороны, не имеет краев, а его род равен 1.
Введенные выше понятия позволяют уточнить определение топологии:
топологией называется раздел математики, изучающий свойства, которые сохраняются при гомеоморфизмах. Важные проблемы и результаты. Теорема Жордана о замкнутой кривой. Если на поверхности проведена простая замкнутая кривая, то существует ли какое-либо свойство кривой, которое сохраняется при деформации поверхности? Существование такого свойства вытекает из следующей теоремы: простая замкнутая кривая на плоскости делит плоскость на две области, внутреннюю и внешнюю. Эта кажущаяся тривиальной теорема очевидна для кривых простого вида, например, для окружности; однако для сложных замкнутых ломаных дело обстоит иначе. Теорема была впервые сформулирована и доказана К.Жорданом (1838–1922); однако доказательство Жордана оказалось ошибочным. Удовлетворительное доказательство было предложено О.Вебленом (1880–1960) в 1905. Теорема Брауэра о неподвижной точке. Пусть D – замкнутая область, состоящая из окружности и ее внутренности. Теорема Брауэра утверждает, что для любого непрерывного преобразования, переводящего каждую точку области D в точку этой же области, существует некоторая точка, которая остается неподвижной при этом преобразовании. (Преобразование не предполагается взаимно однозначным.) Теорема Брауэра о неподвижной точке представляет особый интерес потому, что она, по-видимому, является, наиболее часто используемой в других разделах математики топологической теоремой. Проблема четырех красок. Проблема заключается в следующем: можно ли любую карту раскрасить в четыре цвета так, чтобы любые две страны, имеющие общую границу, были раскрашены в различные цвета? Проблема четырех красок топологическая, так как ни форма стран, ни конфигурация границ не имеют значения.
Гипотеза о том, что четырех красок достаточно для соответствующей раскраски любой карты, была впервые высказана в 1852. Опыт показал, что четырех красок действительно достаточно, но строгого математического доказательства не удавалось получить на протяжении более ста лет. И только в 1976 К.Аппель и В.Хакен из Иллинойского университета, затратив более 1000 часов компьютерного времени, добились успеха.
Односторонние поверхности. Простейшей односторонней поверхностью является лист Мёбиуса, названный так в честь А.Мёбиуса, открывшего его необычайные топологические свойства в 1858. Пусть ABCD (рис. 2,а) – прямоугольная полоска бумаги. Если склеить точку A с точкой B, а точку C с точкой D (рис.
Слово топология
2,б), то получится кольцо с внутренней поверхностью, наружной поверхностью и двумя краями. Одну сторону кольца (рис. 2,б) можно окрасить. Окрашенная поверхность будет ограничена краями кольца. Жук может совершить «кругосветное путешествие» по кольцу, оставаясь либо на окрашенной, либо на неокрашенной поверхности. Но если полоску перед склеиванием концов перекрутить на полоборота и склеить точку A с точкой C, а B с D, то получится лист Мёбиуса (рис. 2,в). У этой фигуры есть только одна поверхность и один край. Любая попытка окрасить только одну сторону листа Мёбиуса обречена на неудачу, так как у листа Мёбиуса всего одна сторона. Жук, ползущий по середине листа Мёбиуса (не пересекая края), вернется в исходную точку в положении «вверх ногами». При разрезании листа Мёбиуса по средней линии он не распадается на две части.  Узлы. Узел можно представлять себе как запутанный кусок тонкой веревки с соединенными концами, расположенный в пространстве. Простейший пример – из куска веревки сделать петлю, пропустить один из ее концов сквозь петлю и соединить концы. В результате мы получим замкнутую кривую, которая остается топологически той же самой, как бы ее ни растягивать или скручивать, не разрывая и не склеивая при этом отдельные точки. Проблема классификации узлов по системе топологических инвариантов пока не решена. Ху Сы-цзян. Теория гомотопий. М., 1964
Узлы. Узел можно представлять себе как запутанный кусок тонкой веревки с соединенными концами, расположенный в пространстве. Простейший пример – из куска веревки сделать петлю, пропустить один из ее концов сквозь петлю и соединить концы. В результате мы получим замкнутую кривую, которая остается топологически той же самой, как бы ее ни растягивать или скручивать, не разрывая и не склеивая при этом отдельные точки. Проблема классификации узлов по системе топологических инвариантов пока не решена. Ху Сы-цзян. Теория гомотопий. М., 1964
Куратовский А. Топология, тт. 1–2. М., 1966, 1969
Спеньер Э. Алгебраическая топология. М., 1971
Александров П.С. Введение в теорию множеств и общую топологию. М., 1977
Келли Дж. Общая топология. М., 1981
Слово топология
Слово топология английскими буквами(транслитом) — topologiya
Слово топология состоит из 9 букв: г и л о о о п т я
Значения слова топология. Что такое топология?
Топология
Тополо́гия (от др.-греч. τόπος — место и λόγος — слово, учение) — раздел математики, изучающий в самом общем виде явление непрерывности, в частности свойства пространства, которые остаются неизменными при непрерывных деформациях, например…
ru.wikipedia.org
ТОПОЛОГИЯ раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание.
Энциклопедия Кольера
ТОПОЛОГИЯ, раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание.
Энциклопедия Кругосвет
ТОПОЛОГИЯ (от греч. topos-место и logos-слово, учение) в химии. Как мат. дисциплина м. б. разделена на две части: теоретико-множественную топологию и геометрическую топологию.
Химическая энциклопедия
Топология — (топо + греч. logos – слово, учение, наука) – раздел математики, изучающий инвариантные свойства пространства. В психологии термин относится к теории поля К.Левина и в аргументах Ж.
Жмуров В.А. Большой толковый словарь терминов по психиатрии
ТОПОЛОГИЯ Отрасль математики, которая занимается теми свойствами пространства, которые остаются неизменяемыми, когда пространство искажается. В психологии эти принципы используются в нескольких областях…
Оксфордский словарь по психологии. — 2002
Топология Зарисского
Тополо́гия Зари́сского — специальная топология, отражающая алгебраическую природу алгебраических многообразий. Названа в честь Оскара Зарисского и, начиная с 1950-х годов, занимает важное место в алгебраической геометрии.
ru.wikipedia.org
Общая топология
Общая топология, или теоретико-множественная топология — раздел топологии, в котором изучаются понятия «непрерывности» и «предела» в наиболее общем смысле. Традиционный подход к общей топологии — теоретико-множественный.
ru.wikipedia.org
ОБЩАЯ ТОПОЛОГИЯ — ветвь геометрии, посвященная исследованию непрерывности и предельного перехода на том естественном уровне общности, к-рый определяется природой этих понятий.
Математическая энциклопедия. — 1977-1985
Сетевая топология
Сетевая топология — термин употребляться для обозначения двух понятий: физической топологии и логической топологии. Топология (от греч. tоpos — место и ¼логия) — часть геометрии, посвященная изучению феномена непрерывности…
Энциклопедический фонд России
Алгебраическая топология
Алгебраи́ческая тополо́гия (устаревшее название: комбинаторная топология) — раздел топологии, изучающий топологические пространства путём сопоставления им алгебраических объектов (групп, колец и т.д.)…
ru.wikipedia.org
Комбинаторная топология, часть топологии, в которой топологические свойства геометрических фигур изучаются при помощи их разбиений на более элементарные фигуры (например, разбиение полиэдров на симплексы) или при помощи покрытий системами множеств.
БСЭ. — 1969—1978
КОМБИНАТОРНАЯ ТОПОЛОГИЯ — раздел топологии, в к-ром топологич. свойства геометрич. фигур ивучаются при помощи их разбиений на более элементарные фигуры (напр., разбиение полиэдров на симплексы) или при помощи покрытий системами множеств.
Математическая энциклопедия.
— 1977-1985
Шина (топология компьютерной сети)
Топология типа общая ши́на, представляет собой общий кабель (называемый шина или магистраль), к которому подсоединены все рабочие станции. На концах кабеля находятся терминаторы, для предотвращения отражения сигнала.
ru.wikipedia.org
Компьютерная ши́на (от англ. computer bus, bidirectional universal switch — двунаправленный универсальный коммутатор) — в архитектуре компьютера подсистема, которая передаёт данные между функциональными блоками компьютера.Современные компьютерные шины используют как параллельные, так и последовательные соединения и могут иметь параллельные (multidrop) и цепные (daisy chain) топологии.
ru.wikipedia.org
База топологии
Объекты, определённые в терминах баз Упорядоченная топология обычно определяется как топология порождённая набором открыто-интервальных множеств.
ru.wikipedia.org
Русский язык
Топ/о/ло́г/и/я [й/а].
Морфемно-орфографический словарь. — 2002
Примеры употребления слова топология
В Cray XC30 используется масштабируемая архитектура Adaptive Supercomputing, внутренние соединения Aries, топология сети Dragonfly.
Делинь работает на стыке многих математических областей, считая наиболее интересной для себя задачей объединение таких направлений как топология, теория групп и теория мотивов, которую разрабатывал его учитель Александр Гротендик.
FILED UNDER : IT