На главнуюМатематический разделКриптография и т.д.Новости

Рекуррентные соотношения — соотношения вида «следующий через предыдущих», то есть отношение, когда значение f(n) описывается через f(m), где n > m. f — функция целого аргумента, обычно натурального или целого неотрицательного.

Должны быть известны некоторые начальные условия, за счёт которых вычисление значения f будет без зацикливания.

В общем случае рекуррентное соотношение записывается в виде g(n) = f(n, g(n-1), g(n-2), …, g(n-k)), где k — порядок рекуррентного соотношения.

Для рекуррентного соотношения порядка k должны быть хотя бы k начальных условий вида g(x)=y, где x, y известны, например, известны значения g(0), g(1), …, g(k-1).

Пример: i-ый член арифметической прогрессии может определяться как a(i) = a(i — 1) + d. В качестве начального условия выступает первый член прогрессии, а порядок k = 1.

Другой пример:

Эта немного страшная формула определяет так называемые числа Фибоначчи, то есть последовательность натуральных чисел, где каждое число есть сумма двух предыдущих. Порядок данного рекуррентного соотношения равен 2, соответственно требуется два начальных условия.

Для прогеров аналогом рекуррентных соотношений являются рекурсивные функции. Если f — рекурсивная функция, то при вычислении её значения выполняются вызовы самой же f. В реализацию рекурсивной функции обязательно входят так называемые граничные условия. Если они не прописаны, неизбежно возникает переполнение стека, поскольку память ЭВМ всегда конечная.

Рекуррентные соотношения необязательно реализуются с помощью рекурсивных функций.

Рекуррентные соотношения.

Пример, когда рекуррентное соотношение реализовано без рекурсии, можно скачать тута.

Яркий пример использования рекуррентных соотношений в криптографии — формулы для псевдослучайных генераторов. В частности, на данном сайте в статье про теорию случайных генераторов рассматриваются линейный конгруэнтный и BBS-генератор, определяемые именно с помощью рекуррентных соотношений. У энтузиастов всегда есть право попытаться составить формулы генераторов, выдающие то же самое без рекуррентных соотношений.

Иногда задание n-го члена ряда как функции от n неудобно. Например, эта ситуация имеет место, когда требуется найти сумму первых k членов ряда, при этом формула для n-го члена содержит такие штуки, как степени, факториалы.

В случаях вроде только что названного поступают так: первый член ряда берут как начальное условие. Составляют формулу вида g(n) = a(n+1)/a(n). Далее равенство a(n+1) = a(n) * g(n) берут как рекуррентное соотношение.

Допустим, n-ый член ряда определяется по такой вот страшной формуле:

Скажем, нужно найти сумму этак 50-100 членов ряда. Попробуем «в лоб» написать прогу, которая это делает (идиоты могут считать и вручную, кто же против-то?). Выходит, что в цикле складываем a(i), i = 1, 2, …, вычисляя a(i) по значению i и не используя при этом значения предыдущих членов ряда:

double fact(int n) { … /* реализуем вычисление факториала */ }

double a(int i) { return pow(2, n) / fact(n); }

double StupidFuncSum(int n) {

double sum = 0;

for(int i = 1; i <= n; i++) sum += a(i); return sum; } Чем это плохо? Как минимум много лишних операций. Плюс факториалы больших чисел, как и высокие степени, — вещи с большой погрешностью, да и риск переполнения переменных есть. А теперь без лобовых атак) Действуем вот как:

Граничное условие: a(1) = 2. Через a(1) вычисляем a(2), через a(2) определяем a(3) и т.д. В итоге ни степеней, ни факториалов мы не вычисляем — вот как нам помогает рекуррентное соотношение:

double MegoFunc() {

double sum = 0, cur = 2;

for(int i = 1; i <= n; i++)
{
    sum += cur;
    cur = (2.0 * cur / (i + 1.0));
}

return sum; }

copyright © Исканцев Н.В., 2012

К математическому разделу
На главную

Решение рекуррентных соотношений

Производящие функции наиболее часто применяются при решении рекуррентных соотношений. Рекуррентные соотношения, в свою очередь, часто возникают в дискретной математике и комбинаторике, поэтому метод производящих функций для решения рекуррентных соотношений изучают именно в рамках этих дисциплин. Самые простыепримеры решения рекуррентных соотношений приводятся в этой лекции. Более сложные примеры — в последующих лекция.

Общая схема

Пусть последовательность (a₀, a₁, a₂, …) удовлетворяет некоторому рекуррентному соотношению. Мы хотим получить выражение для a_n (при n≥0) в замкнутом виде (если это возможно). Производящие функции позволяют делать эту работу почти механически по одному и тому же алгоритму. Рассмотрим общую схему на простом примере, который позволит продемонстрировать базовые приёмы работы.

Задано линейное однородное рекуррентное соотношение порядка 2 с постоянными коэффициентами:

Порядок соотношения — это его «глубина», то есть количество предшествующих элементов, требуемых для вычисления элемента с номером n. В данном случае порядок равен 2, так как для вычисления a_n требуется знать a_n-1 и a_n-2.

Попытаемся для начала «угадать» ответ:

по данной таблице трудно что-либо сказать сразу, если вы, конечно, не видели этой последовательности раньше и не обладаете достаточным опытом разгадывания такого рода комбинаций.

Значит самое время воспользоваться техникой производящий функций.

Будем искать производящую функцию последовательности в виде

с этой целью умножим верхнюю строчку в записи рекуррентного соотношения на z⁰, следующую — на z¹ и последнюю — на zⁿ:

Теперь сложим все уравнения для всех значений n:

Левая часть уравнения в точности равна G(z), а в правой части есть суммы, очень похожие на функцию G(z), но не равные ей. Эти суммы нужно любым законным способом (используя правила работы с алгебраическими выражениями) привести к виду G(z). Начнём с первой:

Равенство (1) получатся вынесением z в первой степени за знак суммы, это необходимо, чтобы уровнять степень переменной z и индекс переменной a внутри суммы. Действие (2) — изменение индекса суммирования, которое позволяет избавиться от n-1. Равенство (3) получается, если прибавить и снова отнять значение a₀, чтобы получить полную сумму от n=0 до ∞. Равенство (4) справедливо в силу того, что a₀=0.

Аналогичные манипуляции со второй суммой дают нам выражение

Теперь наше исходное уравнение для производящей функции принимает вид:

откуда получаем производящую функцию последовательности в замкнутом виде —

Отыскав производящую функцию в замкнутом виде, её нужно снова разложить в ряд. Это можно сделать разными способами, но самый простой из них — разбить всю дробь на простые дроби и применить формулу для разложения 1/(1-z).

Т. Н. Матыцина ДИСКРЕТНАЯ МАТЕМАТИКА РЕШЕНИЕ РЕКУРРЕНТНЫХ СООТНОШЕНИЙ. Практикум

Итак, разложим знаменатель функции на множители:

Теперь разобьём дробь на сумму простых дробей:

Вспомним разложение для простейшей рациональной функции:

Из этого разложения следует, что (см. также таблицу производящих функций)

Таким образом,

С другой стороны, мы искали G(z) в виде

поэтому, в силу равенства рядов, a_n=3ⁿ-2ⁿ (для n≥0). Теперь скажите: как проверить правильность полученного ответа?

Алгоритм

Алгоритм получения замкнутого выражения для чисел a_n, удовлетворяющих рекуррентному соотношению, с помощью производящих функций состоит из 4 шагов.

1. Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен k):
   
2. Домножить каждую строчку на z в соответствующей степени и просуммировать строчки для всех n≥0.
3. В полученном уравнении привести все суммы ∑ к замкнутому виду. Получить уравнение для производящей функции.
4. Выразить G(z) в явном виде (решить уравнение, полученное на предыдущем шаге) и разложить производящую функцию в ряд по степеням z.

Числа Фибоначчи

Это классический пример, который приводят почти везде, где речь идет о решении рекуррентных соотношений. Рассмотрим рекуррентное соотношение для чисел Фибоначчи:

Это хорошо известная последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:

Эти числа очень быстро растут, например, f₁₀=55, f₂₀=6765, f₃₀=832040, f₁₀₀=354224848179261915075.

Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:

Складываем все строчки:

Третий шаг алгоритма требует привести все суммы к замкнутому виду:

откуда получаем замкнутое выражение для производящей функции:

Осталось «всего лишь» разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:

Таким образом (проверьте),

Как теперь поступить с этими выражениями? Ведь пока нам известно разложение только одной рациональной функции:

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на z₁:

Аналогично (но с делением на z₂) поступим со второй дробью:

Таким образом,

и, следовательно,

Данное выражение можно «причесать», если обратить внимание на то, что 1/z₁=-z₂, 1/z₂=-z₁ и z₁-z₂=√5 (корень из 5):

Если записывать формулу в терминах хорошо известного «золотого сечения»

то, обозначив , получим

Если «золотое сечение» не использовать, то лучше всего формула выглядит в следующем виде:

чего достаточно трудно было ожидать, глядя на красивое исходное рекуррентное соотношение.

Обязательно проверьте формулу хотя бы для n=0, 1, 2. Как изменится производящая функция и конечная формула, если положить f₀=f₁=1?

Более сложное соотношение

Рассмотрим довольно произвольное рекуррентное соотношение:

Рассчитаем несколько первых элементов:

Несколько следующих действий мы выполним без пояснений, поскольку они абсолютно аналогичны тем, которые уже делались раньше:

Пока непонятно, что делать с последней суммой. Как её «замкнуть»? На самом деле, очень просто, если вспомнить про производную (подробнее см. лекцию «Преобразование производящих функций: полиномиальный множитель и делитель»):

поэтому

Обратите внимание, что мы вынесли производную за знак бесконечной суммы, не проверив, имеем ли мы на это право. Можно показать, что все сделано законно, но мы не будем этим заниматься сейчас. Последняя сумма может быть свёрнута:

Подставив свёрнутое выражение обратно, имеем,

Таким образом, наше последнее уравнение примет вид

Это уравнение для производящей функции.

Из него выражаем G(z):

Довольно страшное выражение, которое нам предстоит разложить в ряд, на самом деле только кажется таким. Разложим знаменатель на множители и разобьём дробь на сумму простых дробей:

Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее (см. также «Расширенные биномиальные коэффициенты»):

Теперь соберём ответ:

Значит,

Подстановка первых пяти значений совпадает с числами из таблицы, в которую мы их записали в начале.

↑ наверх ↑

вернуться к содержанию

ПРОИЗВОДЯЩАЯ ФУНКЦИЯ. ЧИСЛА ФИБОНАЧЧИ. РЕШЕНИЕ ПРОСТЕЙШИХ РЕКУРЕНТНЫХ СООТНОШЕНИЙ

Производящая функция  последовательности  — это формальный степенной ряд

Числа Фибоначчи – это последовательность  чисел

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

в которой каждое последующее число равно сумме двух предыдущих.

Более формально, последовательность чисел Фибоначчи 
  задаётся  линейным рекуррентным соотношением:

 

Покажем здесь,  как  аналитически построить  производящую функцию для чисел Фибоначчи.

Алгоритмы рекуррентных соотношений

Пусть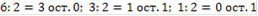 

производящая функция чисел Фибоначчи. Имеем

Если  из первой строки  вычтем  вторую  и третью, то, поскольку

получим выражение

Следовательно,

Рациональную дробь
 представим в виде

где  находятся из уравнения ,  а числа  являются  решением системы уравнений
Далее,  используя ряд

получаем, что

Следовательно,

 

В результате мы нашли, что n- ое число Фибоначчи имеет вид

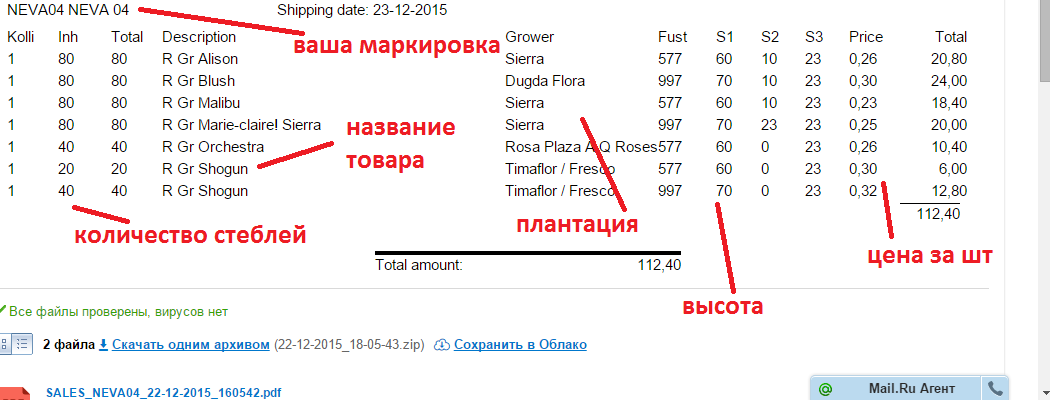
Найдем числа    Имеем

Если разделим это равенство на , то в результате получим

Следовательно,    являются корнями уравнения

Решая его получаем

Решая систему

 

 

получаем, что

В результате получаем

 

Упражнение.  Используя  рассмотренный способ решения построить производящую функцию последовательности,  удовлетворяющей следующему рекуррентному соотношению

и начальным условиям

a)    

b)   

Решение.a)

Выпишем производящую функцию

Используя  соотношение
получаем, что производящая функция  удовлетворяет уравнению

Следовательно,

 где  находятся из уравнения ).

Разложим на две простые дроби и используя ряд  , получаем

Подставив начальные условия  получаем,

Отсюда следует:

Ответ.

a)

 

 

 

 

Пример 4.1. Показать, что общее решение рекуррентного уравнения

f (n+2) = 7∙f (n+1) — 12∙f (n)

можно записать в виде

.

Легко проверить, что последовательность f (n) при любых значениях произвольных констант обращает заданное рекуррентное уравнение в тождество, т.е. первое требование к общему решению удовлетворяется. Действительно,

Чтобы убедиться в выполнении второго требования, выберем в качестве начальных условий произвольные числа A, B, т.е.

f(0 ) = A,

f (1) = B.

Решение рекуррентных соотношений

Так как из предполагаемого общего решения имеем

, ,

то для нахождения постоянных используем систему линейных уравнений

Решая эту систему, получим аналитические выражения для искомых величин

.

Из полученных выражений следует — для любых начальных условий A, B существует единственная последовательность

,

удовлетворяющая этим условиям и самому рекуррентному уравнению, что подтверждает выполнение второго требования к общему решению.

Пример 4.2. Найти общие решения однородных рекуррентных уравнений

a) f (n+3) – 9 f (n+2) + 26 f (n+1) – 24 f (n) = 0,

б) f (n+4) – f (n) = 0,

в) f (n+3) + 6 f (n+2) + 12 f (n+1) + 8 f (n) = 0,

г) f (n+4) + 2 f (n+2) + f (n) = 0.

a) Характеристическое уравнение, соответствующее первому из заданных рекуррентных уравненений,

,

имеет три различных действительных корня

.

В соответствии с правилом 1 функции натурального аргумента

составляют фундаментальную систему решений.

В итоге общее решение рекуррентного уравнения имеет вид

.

б) Характеристическое уравнение

имеет четыре различных корня:

два комплексных сопряженных ;

два действительных .

В соответствии с правилами 1, 2 четыре линейно независимые функции натурального аргумента

в которых b = p/2, составляют фундаментальную систему решений.

Следовательно, искомое общее решение рекуррентного уравнения имеет вид

.

в) Характеристическое уравнение

имеет один корень h = — 2 кратности m = 3.

Согласно правилу 3, фундаментальную систему решений составляют три функции натурального аргумента

и, как следствие, искомое общее решение рекуррентного уравнения записывается в виде равенства

.

г) Характеристическое уравнение

имеет два комплексных сопряженных корня кратности m = 2. В этом случае, согласно правилу 4, фундаментальная система решений включает четыре линейно независимые функции натурального аргумента

в которых b = p/2 , и общее решение однородного рекуррентного уравнения имеет вид

.

Пример 4.3. Найти частное решение рекуррентного уравнения

для следующих вариантов правых частей:

a) а = 5, d (n) = 12,

б) а = — 2, d (n) = 4 (30n + 7),

в) а = 3, d (n) = 2.

Запишем характеристический многочлен

,

который является общим для всех вариантов исходных данных и имеет три различных действительных корня

.

а) Число а = 5 не относится к корням характеристического многочлена (R (5) = 6). Учитывая, что полином d (n) = 12 в правой части имеет нулевой порядок, записываем (в соответствии с правилом 1) аналитический вид частного решения и подставляем его в исходное уравнение. В результате будем иметь равенство

,

из которого находим D = 2, т.е. искомое частное решение можно записать в виде

.

б) Число а = — 2 также не относится к корням характеристического многочлена ( R (-2) = — 120 ). В данном случае полином d (n) имеет первый порядок, т.е. согласно правилу 1, неизвестный полином D (n), входящий в частное решение, можно записать следующим образом

D (n) = An + B,

где A, B — неопределенные коэффициенты. Подставим частное решение в рекуррентное уравнение

и преобразуем полученное выражение с учетом равенств

D ( n + 1 ) = A∙n + ( A + B ),

D ( n + 2 ) = A∙n + ( 2A + B ),

D ( n + 3 ) = A∙n + ( 3A + B ),

в результате чего будем иметь

.

Приравнивая коэффициенты при одинаковых степенях n (при нулевой и первой), получим систему уравнений

— 120 А = 120,

-148 А – 120В = 28,

разрешая которую, находим A = -1, B = 1, т.е. искомое частное решение можно записать следующим образом

.

в) Число а = 3 является простым (однократным) корнем характеристического многочлена. Для данного варианта исходный полином d (n) = 2 .

Записываем, согласно правилу 2, аналитический вид частного решения и подставляем его в исходное уравнение

.

После сокращения на и приведения подобных членов несложно заметить, что будет выполняться равенство

,

где R (3), — значения характеристического многочлена и его производной при h = 3.

Учитывая R (3) = 0, получаем , т.е. D существует, если значение отлично от нуля. Это подтверждает необходимость строгого соблюдения правила 2 (проверки и учета кратности корня).

Так как в рассматриваемом случае , то и искомое решение имеет вид

.

Пример 4.4. Найти решения рекуррентных уравнений с известными начальными условиями:

a) f (n+2) – f (n+1) – f (n) = 0, f (0) = 1, f (1) = 2,

б) f (n+2) – 2 f (n+1) + f (n) = 6n, f (0) = 1, f (1) = 3.

a) Характеристическое уравнение

имеет два действительных корня

, ( А = ).

Следовательно, фундаментальную систему решений составляют две функции натурального аргумента

, ,

а общее решение имеет вид

.

Вычисляем необходимые значения функций ( n = 0,1 ):

, , ,

и записываем систему линейных уравнений относительно неизвестных значений произвольных постоянных:

Решая эту систему, получим выражения для неизвестных величин

, .

После подстановки последних в общее решение записываем аналитический вид искомого решения, удовлетворяющего заданным начальным условиям:

.

На первый взгляд, кажется удивительным, что это выражение, с помощью которого получаются числа Фибоначчи, для любого n принимает целые значения.

б) Характеристическое уравнение

имеет один действительный корень h = 1 кратности m = 2. Следовательно, фундаментальную систему решений составляют две функции

а общее решение однородного уравнения записывается следующим образом

.

Правая часть рекуррентного уравнения, согласно условиям примера, имеет вид (4.15) с параметрами

a = 1, d ( n ) = 6 n,

т.е.

a = h = 1 — двукратный корень характеристического уравнения.

Исходя из этого, записываем аналитический вид частного решения

и подставляем его в исходное уравнение

.

После преобразования имеем 6A∙n + 6A + 2B = 6n. Приравнивая коэффициенты при одинаковых степенях n, получаем систему уравнений

6 A = 6,

6 A + 2 B = 0,

разрешая которую, находим A = 1, B = — 3, т.е. частное решение неоднородного уравнения удовлетворяет равенству

,

а с учетом ранее записанного его общее решение имеет вид

.

Для нахождения решения, удовлетворяющего начальным условиям, вычисляем значения функций , , ( n = 0,1 )

=1, =1, =0, =1, , ,

записываем систему линейных уравнений

и, решая эту систему, получаем .

Подставляя полученные значения в общее решение, будем иметь функцию натурального аргумента

f (n) = (n – 3)∙ + 4 n + 1,

представляющую искомое частное решение, удовлетворяющее заданным начальным условиям.