admin / 01.05.2018
Пропорция в искусстве
Пропорции золотого сечения создают впечатление гармонии, красоты. Поэтому скульпторы, архитекторы, художники использовали и используют золотое сечение в своих произведениях
Парфенон
Золотые пропорции присутствуют в размерах фасада древнегреческого храма Парфенона. При его раскопках были обнаружены циркули, которыми пользовались архитекторы
и скульпторы античного мира.


Это древнее сооружение с его гармоническими пропорциями дарит нам такое же эстетическое наслаждение как и нашим предкам. Многие искусствоведы, стремившиеся раскрыть секрет того могучего эмоционального воздействия, которое это здание оказывает на зрителя, искали и находили в соотношениях его частей золотую пропорцию.
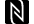
Известен целый ряд пропорций. Так, приняв за 1 ширину торцевого здания, можно получить геометрическую прогрессию, состоящую из восьми членов: расстояние между второй и седьмой колоннами равно , между третьей и шестой — между четвертой и пятой — . Аналогичные закономерности мы видим и в построении здания по высоте. Объединив их, получим прогрессию.
Здесь поучительно вспомнись о пропорциях человеческого тела, отмеченных ранее. Сравнивая, видим, что отношение торцевой длины здания к его высоте равно отношению человеческого роста к длине нижней части тела: 1/. Высота крыши Парфенона относится к расстоянию между крышей и капителями колонн, как : т. е. так же, как отрезок ВС относится к отрезку ЕС.
Эти совпадения не случайны. В своих архитектурных творениях древнегреческие мастера исходили из пропорций, которые видели в природе, и прежде всего в пропорциях человеческого тела.
Портрет Моны Лизы
Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках,
являющихся частями правильного звездчатого пятиугольника.
Золотое сечение в картине И. И. Шишкина»Сосновая роща»

На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины по золотому сечению и дальше.
Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.
Золотая спираль в картине Рафаэля»Избиение младенцев»
В отличии от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре — спирали. Многофигурная композиция, выполненная в 1509 — 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру»Избиение младенцев».
На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается …золотая спираль! Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.

Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции»Избиение младенцев» или только»чувствовал» ее. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел. Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, — в левой части композиции и лежащее тело ребенка — в ее центре. Первоначальную композицию Рафаэль выполнил в рассвете своих творческих сил, когда он создавал свои наиболее совершенные творения. Глава школы романтизма французский художник Эжен Делакруа (1798 — 1863) писал о нем:»В сочетании всех чудес грации и простоты, познаний и инстинкта в композиции Рафаэль достиг такого совершенства, в котором с ним еще никто не сравнился. В самых простых, как и в самых величественных, композициях повсюду его ум вносит вместе с жизнью и движением совершенных порядок в чарующую гармонию». В композиции»Избиение младенцев» очень ярко проявляются эти черты великого мастера. В ней прекрасно сочетаются динамизм и гармония. Этому сочетанию способствует выбор золотой спирали за композиционную основу рисунка Рафаэля: динамизм ему придает вихревой характер спирали, а гармоничность — выбор золотого сечения как пропорции, определяющей развертывание спирали.

Тот же принцип мы видим в картине И.Е. Репина «А.С. Пушкин на акте в Лицее 8 января 1815 года».

Фигура Пушкина помещена художником в правой части картины по линии золотого сечения. Левая часть картины, в свою очередь, тоже разделена в пропорции золотого сечения: от головы Пушкина до головы Державина и от нее до левого края картины. Расстояние от головы Державина до правого края картины разделено на две равные части линией золотого сечения, проходящей вдоль фигуры Пушкина.
Еще один пример — картина Н.Н. Ге «Александр Сергеевич Пушкин в селе Михайловском».

В этой картине фигура Пушкина также поставлена художником слева на линии золотого сечения. Композиционное построение картины подобно картине Репина. Голова военного, с восторгом слушающего чтение поэта, находится на другой вертикальной линии золотого сечения.
Содержание
Основы дизайнерского проектирования / Композиция
Пропорциональность
 Пропорции — это одно из классических средств композиции, с помощью которого достигается организованность формы. Масштаб и пропорции неразрывно связаны между собой. Пропорция — это равенство двух отношений. Размерные отношения элементов формы — это та основа, на которой строится вся композиция. Как бы ни были хороши детали изделия сами по себе, но если всю его объемно-пространственную структуру не объединяет четкая пропорциональная система, трудно рассчитывать на целостность формы.
Пропорции — это одно из классических средств композиции, с помощью которого достигается организованность формы. Масштаб и пропорции неразрывно связаны между собой. Пропорция — это равенство двух отношений. Размерные отношения элементов формы — это та основа, на которой строится вся композиция. Как бы ни были хороши детали изделия сами по себе, но если всю его объемно-пространственную структуру не объединяет четкая пропорциональная система, трудно рассчитывать на целостность формы.
Пропорции интересовали художников во все времена. Об этом свидетельствуют различные пропорциональные системы, обнаруженные позднейшими исследователями в архитектурных сооружениях прошлых эпох — в египетских пирамидах, в греческих храмах, во дворцах и театрах Рима. Это понятно. Пропорции играют исключительную роль в предметном пластическом искусстве. О пропорциях как средстве гармонизации формы написано, пожалуй, больше, чем обо всех других, вместе взятых. Исследованию пропорций посвящали свои труды ученые, зодчие и художники античности и эпохи Ренессанса (Витрувий, Палладио, Виньола, Серлио и многие другие).
Пропорции в композиционной структуре произведения искусства
Знали силу этого средства и в совершенстве владели им многие мастера-ремесленники— эти инженеры и дизайнеры своего времени, создававшие прекрасные станки, машины, часы, светильники, мебель. Формы вещей XIV—XV вв. и более позднего времени нередко поражают совершенством своих пропорций.
Без пропорций немыслимы процесс гармонизации композиции и решение идейно-образных задач. Вольно или невольно, интуитивно или с помощью математических расчетов и геометрических построений художник, создавая композицию, оперирует теми или иными отношениями элементов композиции между собой и с целым. Каждое здание жилого или общественного назначения, каждое промышленное изделие имеет свои пропорции. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Пропорциональные величины — величины, зависящие друг от друга таким образом, что с увеличением одной из них в несколько раз соответственно во столько же раз увеличивается другая величина. В противном случае пропорции нарушаются. Размерные отношения элементов формы — это та основа, на которой строится вся композиция. Как бы ни были сами по себе хороши детали изделия, но если всю его объемно-пространственную структуру не объединяет четкая пропорциональная система, трудно рассчитывать на целостность формы. Пропорционирование следует рассматривать как творческий процесс, поэтому каждое сооружение, каждое промышленное изделие представляет целую систему размерных отношений, определяющую функциональное назначение предмета. Нельзя пропорционировать, скажем, станок, прежде чем определится его кинематическая схема. Пропорция учитывает конкретные условия, место и назначение предмета. В предметном мире, как и в мире природы, все должно быть взаимосвязано пропорциями.
Пропорции имеют большое художественное значение. Они определяют соразмерность и гармоничность элементов формы, всех ее частей друг с другом и с целым.
Выразительными или гармоничными пропорциями могут обладать как статуя, архитектурное сооружение, книжная обложка, так и объект дизайна. Пропорции — одно из составляющих выразительности объекта, они как-то обозначают его характер. Поэтому пропорционирование, т. е. приведение всех частей и деталей целого в определенный пропорциональный строй, является средством гармонизации.
В практике встречаются в основном два вида пропорциональных отношений — арифметические (целочисленные пропорции) и геометрические (иррациональные пропорции). Простые арифметические пропорции можно выразить в целых числах. Среди геометрических фигур с простыми целочисленными отношениями сторон — квадрат (1:1), прямоугольник в два квадрата (1:2). Особый интерес представляет прямоугольный треугольник с отношениями сторон 3:4:5. В Древнем Египте этот треугольник считался священным. С одной стороны, он использовался египтянами как основа пропорционального строя при возведении пирамид и храмов, с другой — оказывал практическую помощь в самом процессе строительства.
Посредством этого треугольника можно было легко определить и наметить прямой угол, что было достаточно важно для древнего строителя. Для этого надо было отметить узелками на шнуре двенадцать одинаковых членений и. натянув его в трех точках с интервалами 3, 4, 5, получить прямой угол.
Единство пропорционального строя определяется наличием подобий. Без подобия нет пропорций в классическом понимании этого термина. В связи с этим при пропорционировании создаваемых композиций и исследовании уже существующих произведений широко применяется метод геометрического подобия фигур. Геометрическому подобию фигур, например прямоугольника, всегда сопутствует простейшая пропорция а:б = а:в. При этом, если прямоугольники подобны, их диагонали будут параллельными или же перпендикулярными друг другу. В первом случае оба прямоугольника будут одновременно расположены по вертикали или по горизонтали, во втором случае один прямоугольник располагается по вертикали, другой имеет горизонтальную направленность. Таким образом, находя на каком-либо фронтальном изображении объекта системы параллельных и перпендикулярных линий, являющихся диагоналями прямоугольников, в которые вписываются те или иные элементы композиции, мы можем утверждать, что в данном случае имеет место гармонизация формы на основе геометрического подобия.
Особенно велика роль пропорций в архитектуре. Постижением наилучших отношений величин, математическим анализом уже существующих памятников, поисками «ключа» к их совершенству занимались такие исследователи, как римский архитектор Витрувий, художники Возрождения Леонардо да Винчи, Альберти, Дюрер и более поздние — Жолтовский, Химбидж, Корбюзье и многие другие. Было установлено, что существует много различных математических соотношений, рациональных и иррациональных, которые были положены в основу пропорций самых замечательных памятников.
К наиболее бесспорным относится «золотое сечение». Если выстроить ряд золотого сечения, то соотношение одного отрезка к другому будет иметь постоянную величину. Если взять отрезок за единицу и разделить его в золотом сечении, то больший отрезок будет равен 0,618, а меньший 0,382, и эту операцию (деля меньший отрезок в том же отношении) можно повторять, получая при этом ряд золотого сечения. Практически чаще всего применяется приближенное «золотое сечение», исследованное в XII веке известным итальянским математиком Леонардо из Пизы, прозванным Фибоначчи, которое и названо в честь автора. Это такие соотношения, где каждое последующее число является суммой двух предыдущих: 3:5; 5:8; 8:13; 13:21 и т. д. В этом ряду, начиная с пяти 5:8, 8:13, 13:21 и далее, все отношения будут очень близки к пропорциям золотого сечения, причем чем дальше, тем они будут точнее.
На практике совмещение двух видов пропорциональных отношений (арифметических и геометрических) встречается довольно часто. Даже в знаменитом Парфеноне мы можем наблюдать такие взаимосвязи. Известно, что его фасад без фронтона вписывается в прямоугольник со сторонами 1:2, а по вертикали все основные элементы композиции связаны с пропорциями золотого сечения.
Сделать предмет или выстроить красивый дом по уже известному рецепту было всегда заманчиво. Поэтому увлечение найденными пропорциями, возведение их в некоторый вневременной абсолют было довольно распространенным заблуждением и в других видах искусства, монументальной живописи например.
В предметном мире пропорции приобретают важную роль, когда человек может их реально воспринять, когда, наблюдая предмет, он действительно соотносит какие-то величины. Мы ощущаем пропорции шкафа или холодильника, соизмеряя их высоту и ширину, величину эмблемы и дверцы. Мы ощущаем величину всего предмета по отношению к среде, в которой он находится, например высоту светильника к высоте стены.
В дизайне пропорции складываются обычно в результате корректировки уже определившейся основы. Эта основа обусловлена назначением предмета, технологией его изготовления и проч. Приведем конкретный пример. Мы находим неудовлетворительными пропорции кухонного шкафчика, продиктованные целым рядом практических соображений. Чтобы зрительно изменить эти пропорции, мы расчленяем плоскость на две неравные части и подчеркиваем это разделение контрастным цветосочетанием. Выдвигающийся ящик в верхней части шкафчика служит основой для расчленения плоскости. В другом случае это может быть горизонтальная ручка для открывания дверцы.
Пропорции лишь тогда приобретают действенную силу, когда проектировщик подходит к ним от самой сущности вещи, а не навязывает форме произвольно выбранную пропорциональную схему. Вспомним диалог Сократа и оружейника Пистия. Философ спрашивает оружейника: «Как получается, что ты продаешь больше панцирей, чем другие мастера, хотя делаешь их не более прочными и не более роскошными?» — «Потому, что я делаю их пропорциональными».— «Но ведь бывают непропорциональные фигуры. Как же ты можешь делать «пропорциональные» панцири для «непропорциональных» фигур?» — «А я их подгоняю. Панцирь по мерке и есть панцирь пропорциональный».
предыдущая / главная / следующая страница
10. Пропорции
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.

a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



- Подробности
- Автор: Administrator

Понятие о пропорциях предметов
Любое правдивое изображение какого-либо предмета передает в рисунке или картине его основные, характерные признаки, понятные зрителю.
Если задать себе вопрос, по каким внешним особенностям зритель узнает изображение, долго искать ответ на него не придется.
Каждому из нас понятно, что «узнавание» изображения происходит благодаря переданным художником в произведении именно основным, характерным признакам предметов или явлений. Безусловно, такой передаче признаков способствуют многие факторы реалистического изображения: перспективные построения, светотеневые отношения, фактура поверхности и т.д.
Что же такое признаки предмета? Это свойства предмета, его приметы. На языке изобразительного искусства отличительные черты объектов рисования называются пропорциями и конструкцией.
Пропорции (лат. proportio — соразмерность) — соразмерность всех частей художественного произведения или архитектурного сооружения, их соответствие друг другу и определенное соотношение с целым.
Конструкция (лат. constructio — оставление, построение) — строение, взаимное расположение частей предмета, структура его формы.
Красота предмета образуется пропорциями, становясь строгой соразмерностью, гармонией всех частей, такой, что ни прибавить, ни убавить ничего нельзя, и все детали, части должны взаимно соответствовать друг другу.
Итак, в окружающем нас мире все предметы характеризуются не только конструктивным строением, но и размерами. Возьмем, например, садовую лейку — предмет сложной комбинированной формы с неполной симметрией частей (рис. 13). При рисовании лейки с натуры важно увидеть, что две ее части — трубка и ручка — расположены в одной вертикальной плоскости, проходящей через ось симметрии цилиндрического корпуса, и тогда в зависимости от поворота модели не будет допущена ошибка при построении изображения. Одновременно рисовальщик обязан следить за соотношением основных величин предмета — его высотой и шириной, определяя их на глаз.
Натурные постановки из двух и более предметов заставляют рисовальщика учитывать пропорциональные отношения между ними. Например, при рисовании с натуры цветущих комнатных растений (возьмем кактус опунция и бегонию крупнолистную) из-за различных размеров внимание рисующего непременно сосредоточивается на их соотношениях, а при построении рисунка — на своеобразной композиционно-пластической и конструктивной выразительности. На этой основе образуются представления о натуре, организовываются в изображении ее объемно-пространственные свойства, пропорциональность, пластичность.

Рис.
13
Грамотный рисунок — это прежде всего изображение пропорций предмета. Но это не значит, что предмет надо непременно рисовать в натуральную величину. Это невозможно, если принять во внимание наше зрительное восприятие, и не нужно, если учитывать расстояние от вашего места до натуры. Иное дело, что размеры предмета выдержаны в пропорциях, а также по отношению к окружающей среде и в любом уменьшенном виде выглядят правдиво. Следовательно, здесь все зависит от выбранного вами масштаба изображения. Это касается также и установления размеров отдельных частей предмета по отношению к общим массам.
Таким образом, выдержать пропорции в рисунке — значит добиться соотношения величин всех частей предмета к целому в пределах формата и выбранного масштаба изображения.
Но пропорции есть не только в соотношении величин предмета. В каждом светотеневом рисунке нужно передать еще и пропорциональные натуре отношения в тоне. Известно, что правдивого изображения натурной постановки рисовальщик достигает на основе передачи как раз взаимных отношений по светлоте. Вы уже знаете, что самая светлая на предмете в натуре часть или точка во много раз светлее самой белой бумаги, не говоря уже о карандаше, не способном проложить темного пятна, адекватного пятну в натуре. Что же должен делать в этом случае рисовальщик? Правдивости в тоне добиваются выдержанностью в рисунке тонального масштаба.
Пропорциональных натуре отношений достигают благодаря учету белизны бумаги и кроющей силе карандаша. А за основу таких отношений берут, например, блик и самое темное пятно в тени, сравнивая в рисунке с ними все остальные градации светотени. Умелое владение тоном завершает правдивую передачу натурной постановки.
При изложении понятия о пропорциях предметов нужно подробнее остановиться на так называемом «золотом сечении». Сведения о нем восходят ко времени расцвета античной культуры и упоминаются в трудах великих древнегреческих мыслителей Пифагора, Платона, Евклида. До сих пор считается, что понятие о золотом делении ввел в научный обиход в VI в. до н.э. философ и математик Пифагор, позаимствовавший, вероятно, знание его у египтян и вавилонян, широко применявших это красивое пропорциональное соотношение величин при создании пирамид, храмов, рельефов, пальметок. Волею судьбы Пифагор посетил землю фараонов, где увидел нечто его глубоко поразившее, затем был пленен персами, от которых попал в Вавилон. Тамошние жрецы помогли любознательному греку изучить теорию чисел, музыку, философию. Вернувшись в зрелом возрасте на родину, Пифагор основал в городе Кротоне общество математиков и философов, занимавшихся не только геометрией и наукой мудрости, но и теорией музыки. Пифагор открыл знаменитое математическое соотношение: квадрат гипотенузы равен сумме квадратов катетов.
Если Пифагор позаимствовал золотую пропорцию у египтян, то последние, вероятно, переняли ее у более древних предшественников, о которых мы уже, к сожалению, никогда не узнаем. Древний мир загадочен, и вот новые доказательства этого: при археологических раскопках палеолитической стоянки на реке Ангаре в Сибири была найдена пластинка из бивня мамонта с рисунком-календарем на ее поверхности. Удивляют размеры пластинки (13,6*8,2 см), с точностью до 1 мм отвечающие золотой пропорции. Возможно это случайность, но впечатляющая. Как тут не подумать о том, что законы красоты — в соизмеримости формы: эта пластинка для человека эпохи позднего каменного века только в таком соотношении сторон была приемлемой.
Предисловие: золотое сечение — красивая математическая концепция
Наш далекий предок, конечно, не мог знать о закономерностях зрительного восприятия и эмоционального воздействия вещи. Интуитивное познание мира привело человека, жившего 15 тысяч лет назад, к неожиданному для современной науки результату. Почему же тогда подобные пропорции выдерживались в разных других предметах и изображениях, найденных археологами?
Например, пропорции «золотого сечения» обнаружены в некоторых первобытных фресках пещер Франции, Испании и Швейцарии, в наскальных рисунках близ села Шишкино на реке Лене. Все это было бы странным, если бы не оказалось закономерным: наблюдательность человека подсказала ему эту пропорцию на основе природных проявлений данного соотношения. Поистине «божественная» назвал эту пропорцию современник великого Леонардо да Винчи монах-математик Лука Пачоли. И вообще, вся история учения о пропорциях связана с поисками теории гармонии и красоты. Античная эстетика и эстетика Ренессанса искали законы красоты в соотношениях отдельных частей и целого. Эти соотношения в формах предметов дают симметрия и золотая пропорция. Пропорции золотого сечения» и симметрия позволяют бесконечно разнообразить композиционные построения в произведениях искусства всех родов и видов.
Математики разных веков объяснили, изучили и глубоко проанализировали золотую пропорцию. Из пропорции вытекает, что если высоту или длину формата бумаги, картины разделить на 100 частей, то больший отрезок «золотого сечения» равен 62 частям, а меньший — 38. Эти три величины — целое, больший отрезок, меньший отрезок — позволяют построить нисходящий ряд отрезков: 100 — 62 = 38; 62 — 38 = 24; 38 — 24 = 14; 24 — 14 = 10. Значит, для художника числа 100, 62, 38, 24, 14, 10 являются рядом величин «золотого сечения», выраженных арифметически. Достаточно убедиться в этом при анализе, например, любого произведения Рафаэля: здесь все подчинено бесконечному разнообразию чисел золотого деления. Рафаэль, возможно, в процессе создания своих композиций использовал циркуль-измеритель, изготовленный из двух деревянных планок и скрепленный одной осью, находящейся на линии «золотого сечения» (62, 38). При работе этого циркуля длинные и короткие концы все время дают требуемое соотношение пропорциональных отрезков.
Благодаря повторению равных, чередованию равных и неравных величин в пропорциях «золотого сечения» в рисунке или картине создастся определенный ритмический строй, втягивающий зрителя в рассматривание изображения. О картинах Рафаэля убедительно сказал выдающийся художник Кузьма Сергеевич Петров-Водкин: «К Рафаэлю… приходишь как на отдых. Эта нежная ясность, детская гениальная шаловливость с цветом и формой, то беззаботно жизнерадостная, то задумчивая и грустная…— она обезоруживает вас, распускает напряженные мускулы. Как совершенный в своих силах, Рафаэль не боится… композиционных канонов».
Но если даже. Рафаэль повторял и чередовал все величины в золотой пропорции лишь благодаря гениальному композиционному чутью и интуиции, то остается констатировать, что так устроила единство мозга и глаза человека сама природа, которая к тому же как бы приложила «божественную» пропорцию к себе самой.
Итальянский математик Леонардо из города Пизы, более известный под прозвищем Фибоначчи (сын Боначчи), в 1202 г. написал математический труд под названием «Книга об абаке» (абакой называли счетную доску), в котором собрал все известные тогдашним любителям счета задачи. Там, например, одна задача была связана с вопросом «Сколько пар кроликов в один год от одной пары рождается?» Поразмыслив на тему кроликов, Фибоначчи выстроил знаменитый ряд цифр: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 277, 610 и т.д. Особенность этого ряда такова, что каждый его член, начиная с третьего, равен сумме двух предыдущих: 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13 + 21 = 34; 21 + 34 = 55; 34 + 55 = 89 и т.д. (Это отношение же чисел ряда Фибоначчи все больше и больше приближается к отношению «золотого сечения» (21 : 34 = 0,617; 34 : 55 = 0,618). Таким образом, суммы, полученные Леонардо Фибоначчи, примечательны тем, что отношение рядом расположенных чисел в пределе стремится к золотой пропорции.
Что касается ряда Фибоначчи в качестве задачи, то она оказала косвенное влияние на исследователей растительного и животного мира, приходивших в конце концов к этому ряду как арифметическому выражению закона золотого деления.
Альбрехт Дюрер разработал способ геометрического деления отрезка прямой по «золотому сечению»: ВС = ½ АВ; CD=BC (рис. 14)

Рис. 14
Советский художник А. Н. Лаптев в 1954 г. написал в сборнике «Вопросы изобразительного искусства» статью «Некоторые вопросы композиции» и в ней, в частности, говорилось: «…Хочу упомянуть о давно известном, особенно в классическом искусстве, законе пропорций «золотого сечения». В силу некоторого свойства нашего зрительного восприятия эти пропорции (примерно 6 к 4) являются наиболее гармоническими и наиболее отвечающими общему понятию красоты и наиболее часто употребляемыми» (М., 1954. С. 66 — 67).
При изложении о пропорциях в рисовании с натуры какого-либо предмета нужно подчеркнуть, что точность определения соразмерных величин зависит от того, как развит глазомер рисующего. Глазомер развивается у каждого при условии систематических занятий изобразительной деятельностью.
<<<предыдущаявверхследующая>>>
FILED UNDER : IT