Умножение матриц

Каталин Дэвид

Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.

Алгоритм умножения матриц

Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.

1. Умножаем элементы первой строки на элементы первого столбца.
   • Умножаем первый элемент первой строки на первый элемент первого столбца.
   • Умножаем второй элемент первой строки на второй элемент первого столбца.
   • Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
   • Складываем полученные произведения.
   • Полученный результат будет первым элементом первой строки произведения матриц.
2. Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
   • Умножаем первый элемент первой строки на первый элемент второго столбца.
   • Умножаем второй элемент первой строки на второй элемент второго столбца.
   • Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
   • Складываем полученные произведения.
   • Полученный результат будет вторым элементом первой строки произведения матриц.
3. Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
4. Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
5. Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.

Пример 7
$A= \begin{pmatrix} 1 & 2 & 2\\ 3 & 1 & 1 \end{pmatrix}$
$B=\begin{pmatrix} 4 & 2 \\ 3 & 1 \\ 1 & 5\\ \end{pmatrix}$

Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.

$A \cdot B=$ $\begin{pmatrix} \color{red}1 &\color{blue}2 & \color{green}2\\ \color{red}3 &\color{blue}1 & \color{green}1 \end{pmatrix} \begin{pmatrix} \color{red}4 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \\ \color{green}1 & \color{green}5 \end{pmatrix}=$ $\begin{pmatrix} \color{red}{1\cdot4}+\color{blue}{2\cdot3}+\color{green}{2\cdot1} & \color{red}{1\cdot2}+\color{blue}{2\cdot1}+\color{green}{2\cdot5}\\ \color{red}{3\cdot4}+\color{blue}{1\cdot3}+\color{green}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}+\color{green}{1\cdot5} \end{pmatrix}=$ $\begin{pmatrix} 12 & 14\\ 16 & 12\\ \end{pmatrix}$

$B \cdot A = \begin{pmatrix} \color{red}4 &\color{blue}2 \\ \color{red}3 & \color{blue}1 \\ \color{red}1 & \color{blue}5 \end{pmatrix} \begin{pmatrix} \color{red}1 &\color{red}2 & \color{red}2\\ \color{blue}3 &\color{blue}1 & \color{blue}1 \end{pmatrix}=$

$\begin{pmatrix} \color{red}{4\cdot1}+\color{blue}{2\cdot3} & \color{red}{4\cdot2}+\color{blue}{2\cdot1} & \color{red}{4\cdot2}+\color{blue}{2\cdot1}\\ \color{red}{3\cdot1}+\color{blue}{1\cdot3} & \color{red}{3\cdot2}+\color{blue}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}\\ \color{red}{1\cdot1}+\color{blue}{5\cdot3} & \color{red}{1\cdot2}+\color{blue}{5\cdot1} & \color{red}{1\cdot2}+ \color{blue}{5\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 10 & 10 & 10 \\ 6 & 7 & 7 \\ 16 & 7 & 7 \end{pmatrix}$

Заметим, что $A \cdot B \neq B \cdot A$

Пример 8
$A= \begin{pmatrix} 5 & 2 \\ 3 & 1 \end{pmatrix} B= \begin{pmatrix} 4 & 6 \\ 5 & 2 \end{pmatrix}$

$A \cdot B = \begin{pmatrix} \color{red}5 & \color{blue}2 \\ \color{red}3 & \color{blue}1 \end{pmatrix} \cdot \begin{pmatrix} \color{red}4 & \color{red}6 \\ \color{blue}5 & \color{blue}2 \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot4}+\color{blue}{2\cdot5} & \color{red}{5\cdot6}+\color{blue}{2\cdot2} \\ \color{red}{3\cdot4}+\color{blue}{1\cdot5} & \color{red}{3\cdot6}+\color{blue}{1\cdot2} \end{pmatrix} =$ $\begin{pmatrix} 30 & 34\\ 17 & 20 \end{pmatrix}$

$B \cdot A= \begin{pmatrix} \color{red}4 & \color{blue}6 \\ \color{red}5 & \color{blue}2 \end{pmatrix} \cdot \begin{pmatrix} \color{red}5 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \end{pmatrix} =\begin{pmatrix} \color{red}{4\cdot5}+\color{blue}{6\cdot3} & \color{red}{4\cdot2}+\color{blue}{5\cdot1} \\ \color{red}{5\cdot5}+\color{blue}{2\cdot3} & \color{red}{5\cdot2}+\color{blue}{2\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 38 & 14\\ 31 & 12 \end{pmatrix}$

Опять-таки $A \cdot B \neq B \cdot A$.

Пример 9
$A= \begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} B= \begin{pmatrix} 5 & 2 & 1 \\ 4 & 3 & 2 \\ 2 & 1 & 5 \end{pmatrix}$

$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} & \color{red}{1} \\ \color{blue}{4} & \color{blue}{3} & \color{blue}{2} \\ \color{green}{2} & \color{green}{1} & \color{green}{5} \end{pmatrix}=$

$\begin{pmatrix} \color{red}{1\cdot5} + \color{blue}{4\cdot4} + \color{green}{3\cdot2} & \color{red}{1\cdot2} + \color{blue}{4\cdot3} + \color{green}{3\cdot1} & \color{red}{1\cdot1} + \color{blue}{4\cdot2} + \color{green}{3\cdot5} \\ \color{red}{2\cdot5} + \color{blue}{1\cdot4} + \color{green}{5\cdot2} & \color{red}{2\cdot2} + \color{blue}{1\cdot3} + \color{green}{5\cdot1} & \color{red}{2\cdot1} + \color{blue}{1\cdot2} + \color{green}{5\cdot5}\\ \color{red}{3\cdot5} + \color{blue}{2\cdot4} + \color{green}{1\cdot2} & \color{red}{3\cdot2} + \color{blue}{2\cdot3} + \color{green}{1\cdot1} & \color{red}{3\cdot1} + \color{blue}{2\cdot2} + \color{green}{1\cdot5} \end{pmatrix}=$
$=\begin{pmatrix} 27 & 17 & 24\\ 24 & 12 & 29\\ 25 & 14 & 12 \end{pmatrix}$

$B \cdot A = \begin{pmatrix} \color{red}{5} & \color{blue}{2} & \color{green}{1}\\ \color{red}{4} & \color{blue}{3} & \color{green}{2}\\ \color{red}{2} & \color{blue}{1} & \color{green}{5} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{4} & \color{red}{3} \\ \color{blue}{2} & \color{blue}{1} & \color{blue}{5} \\ \color{green}{3} & \color{green}{2} & \color{green}{1} \end{pmatrix}=$ $\begin{pmatrix} \color{red}{5\cdot1} + \color{blue}{2\cdot2} + \color{green}{1\cdot2} & \color{red}{5\cdot4} + \color{blue}{2\cdot1} + \color{green}{1\cdot2} & \color{red}{5\cdot3} + \color{blue}{2\cdot5} + \color{green}{1\cdot1} \\ \color{red}{4\cdot1} + \color{blue}{3\cdot2} + \color{green}{2\cdot3} & \color{red}{4\cdot4} + \color{blue}{3\cdot1} + \color{green}{2\cdot2} & \color{red}{4\cdot3} + \color{blue}{3\cdot5} + \color{green}{2\cdot1}\\ \color{red}{2\cdot1} + \color{blue}{1\cdot2} + \color{green}{5\cdot3} & \color{red}{2\cdot4} + \color{blue}{1\cdot1} + \color{green}{5\cdot2} & \color{red}{2\cdot3} + \color{blue}{1\cdot5} + \color{green}{5\cdot1} \end{pmatrix}=$
$=\begin{pmatrix} 11 & 24 & 26\\ 16 & 23 & 29\\ 19 & 19 & 16 \end{pmatrix}$

Опять-таки $A \cdot B \neq B \cdot A$.

Пример 10
$A= \begin{pmatrix} 5 & 2\\ 3 & 1\\ \end{pmatrix} I_{2}= \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}$

$A \cdot B = \begin{pmatrix} \color{red}{5} & \color{blue}{2}\\ \color{red}{3} & \color{blue}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{0} \\ \color{blue}{0} & \color{blue}{1} \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot1}+\color{blue}{2\cdot0} & \color{red}{5\cdot0}+\color{blue}{2\cdot1} \\ \color{red}{3\cdot1}+\color{blue}{1\cdot0} & \color{red}{3\cdot0}+\color{blue}{1\cdot1} \end{pmatrix} = \begin{pmatrix} 5 & 2\\ 3 & 1 \end{pmatrix}$

$B \cdot A = \begin{pmatrix} \color{red}{1} & \color{blue}{0} \\ \color{red}{0} & \color{blue}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} \\ \color{blue}{3} & \color{blue}{1} \\ \end{pmatrix} =\begin{pmatrix} \color{red}{1\cdot5}+\color{blue}{0\cdot3} & \color{red}{1\cdot2}+\color{blue}{0\cdot1} \\ \color{red}{0\cdot5}+\color{blue}{1\cdot3} & \color{red}{0\cdot2}+\color{blue}{1\cdot1} \end{pmatrix} = \begin{pmatrix} 5 & 2\\ 3 & 1 \end{pmatrix}$

Заметим, что $A \cdot I_{2} = I_{2} \cdot A=A$.

Пример 11
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} I_{3}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{0} & \color{red}{0} \\ \color{blue}{0} & \color{blue}{1} & \color{blue}{0} \\ \color{green}{0} & \color{green}{0} & \color{green}{1} \end{pmatrix}=$

$\begin{pmatrix} \color{red}{1\cdot1} + \color{blue}{4\cdot0} + \color{green}{3\cdot0} & \color{red}{1\cdot0} + \color{blue}{4\cdot1} + \color{green}{3\cdot0} & \color{red}{1\cdot0} + \color{blue}{4\cdot0} + \color{green}{3\cdot1} \\ \color{red}{2\cdot1} + \color{blue}{1\cdot0} + \color{green}{5\cdot0} & \color{red}{2\cdot0} + \color{blue}{1\cdot1} + \color{green}{5\cdot0} & \color{red}{2\cdot0} + \color{blue}{1\cdot0} + \color{green}{5\cdot1}\\ \color{red}{3\cdot1} + \color{blue}{2\cdot0} + \color{green}{1\cdot0} & \color{red}{3\cdot0} + \color{blue}{2\cdot1} + \color{green}{1\cdot0} & \color{red}{3\cdot0} + \color{blue}{2\cdot0} + \color{green}{1\cdot1} \end{pmatrix}=$
$=\begin{pmatrix} 1 & 4 & 3\\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix}$ $B \cdot A = \begin{pmatrix} \color{red}{1} & \color{blue}{0} & \color{green}{0} \\ \color{red}{0} & \color{blue}{1} & \color{green}{0}\\ \color{red}{0} & \color{blue}{0} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{4} & \color{red}{3} \\ \color{blue}{2} & \color{blue}{1} & \color{blue}{5} \\ \color{green}{3} & \color{green}{2} & \color{green}{1} \end{pmatrix}=$

$\begin{pmatrix} \color{red}{1\cdot1} + \color{blue}{0\cdot2} + \color{green}{0\cdot2} & \color{red}{1\cdot4} + \color{blue}{0\cdot1} + \color{green}{0\cdot2} & \color{red}{1\cdot3} + \color{blue}{0\cdot5} + \color{green}{0\cdot1} \\ \color{red}{0\cdot1} + \color{blue}{1\cdot2} + \color{green}{0\cdot3} & \color{red}{0\cdot4} + \color{blue}{1\cdot1} + \color{green}{0\cdot2} & \color{red}{0\cdot3} + \color{blue}{1\cdot5} + \color{green}{0\cdot1}\\ \color{red}{0\cdot1} + \color{blue}{0\cdot2} + \color{green}{1\cdot3} & \color{red}{0\cdot4} + \color{blue}{0\cdot1} + \color{green}{1\cdot2} & \color{red}{0\cdot3} + \color{blue}{0\cdot5} + \color{green}{1\cdot1} \end{pmatrix} =$
$=\begin{pmatrix} 1 & 4 & 3\\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix}$

Опять-таки $A \cdot I_{3} = I_{3} \cdot A = A$.

Примечание:

1. В общем случае умножение матриц некоммуникативно.
2. $A\cdot I_{n} = I_{n} \cdot A = A$ для любой матрицы A, имеющей n столбцов.

МатрицыОпределительРанг матрицыОбратные матрицыМатричные уравненияСистемы уравненийКалькуляторы для матриц

Ceza Doch Cezarja   27.11.10 — 12:24	Помогите,пожалуйста,объясните наиболее понятным языком что такое определитель матрицы и для чего он вообще нужен?Перерыла кучу сайтов нигде не могу найти так, чтобы было понятно.
YHVVH   1 — 27.11.10 — 12:26	wiki:Det
Мария Елена   2 — 27.11.10 — 12:33	Не у каждой матрицы может быть «определитель».
andrewks   3 — 27.11.10 — 12:35	и какие сайты мы рыли? что и где непонятно?
Ceza Doch Cezarja   4 — 27.11.10 — 12:41	Для чего он нужен, определитель? Как объяснить это? Как его находить понятно, формулы ясно, а зачем? Наш преподаватель в универе сказал, что спросит об этом, а я не пойму.
Мария Елена   5 — 27.11.10 — 12:46	(4) Пример из школы: определитель квадратного уравнения — дискриминант. Математика для чайников. Матрицы и основные действия над ними По его «знаку» можно судить о наличии действительных решений.
YHVVH   6 — 27.11.10 — 12:48	ты его спроси раньше об этом. Как учитиель он должен помочь тебе.
YHVVH   7 — 27.11.10 — 12:50	вообще сам определитель ничего не значит, а вот его свойства иногда бывают полезными в решении задач.
DarkWater   8 — 27.11.10 — 12:52	(0)Возможно, имеется в виду это свойство: Квадратная матрица называется вырожденной, если её определитель равен нулю. Для такой матрицы невозможно  построить обратную матрицу.
andrewks   9 — 27.11.10 — 12:56	ну, наверное одно из важных свойств: если определитель не равен 0, то система, выраженная в матрице, имеет единственное решение. и является базисом.
Ceza Doch Cezarja   10 — 27.11.10 — 12:57	Если я об этом его спрошу, то не смогу получить хорошую оценку, наверное. Обидно.
Mikeware   11 — 27.11.10 — 12:57	(10) Ну, видимо, ты ее и не заслужило…
Ceza Doch Cezarja   12 — 27.11.10 — 12:58	То есть определитель сам по себе ничего не может обозначать, верно? Он нужен только благодаря его свойствам?
Mikeware   13 — 27.11.10 — 12:58	деввочко, иди зарабатывай «вдвое больше»
Ceza Doch Cezarja   14 — 27.11.10 — 13:00	Определитель матрицы <math>n\times n</math> равен ориентированному <math>n</math>-мерному объёму параллелепипеда, натянутого на её векторы-строки (или столбцы). Как это понять?
andrewks   15 — 27.11.10 — 13:00	(12) что за сумбур? определитель — это некий инструмент.
Мария Елена   16 — 27.11.10 — 13:01	В (5) ошибка.
Ceza Doch Cezarja   17 — 27.11.10 — 13:05	Для чего нужен определитель? Как его использовать?
Мария Елена   18 — 27.11.10 — 13:05	(14) wiki:Векторное_умножение#.D0.92.D1.8B.D1.80.D0.B0.D0.B6.D0.B5.D0.BD.D0.B8.D0.B5_.D0.B4.D0.BB.D1.8F_.D0.B2.D0.B5.D0.BA.D1.82.D0.BE.D1.80.D0.BD.D0.BE.D0.B3.D0.BE_.D0.BF.D1.80.D0.BE.D0.B8.D0.B7.D0.B2.D0.B5.D0.B4.D0.B5.D0.BD.D0.B8.D1.8F_.D0.B2_.D0.B4.D0.B5.D0.BA.D0.B0.D1.80.D1.82.D0.BE.D0.B2.D1.8B.D1.85_.D0.BA.D0.BE.D0.BE.D1.80.D0.B4.D0.B8.D0.BD.D0.B0.D1.82.D0.B0.D1.85
andrewks   19 — 27.11.10 — 13:06	(17) ну, например, при решении СЛУ
Мария Елена   20 — 27.11.10 — 13:08	Как вуз называется?
Ceza Doch Cezarja   21 — 27.11.10 — 13:09	МаГУ, я на заочном, поэтому…
andrewks   22 — 27.11.10 — 13:13	(21) Уважаемая Дочь Цезаря! А теорию вам там не дают что-ли?
Ceza Doch Cezarja   23 — 27.11.10 — 13:16	Преподаватель посчитал, что мы в состоянии сами справится с этим вопросом. По теории он нам дал определение матрицы, свойства определителей, и формулу нахождения определителя 2 порядка. А остальное должны найти сами. Найти-то можно, но хотелось бы ещё и разобраться в этом всём.
Mikeware   24 — 27.11.10 — 13:27	В Челябинске — учиться в МаГУ на завочке — это, имхо, само по себе диагноз…
Ceza Doch Cezarja   25 — 27.11.10 — 13:28	Спасибо вам огромное, я учту, свой диагноз…
gr13   26 — 27.11.10 — 13:36	к примеру по детерминант нужен для определения и нахождения обратной матрицы. один способ через ajective матрицу и детерминант ты находишь обратную. И если хочешь определиться возможно ли найти обратную матрицу или нет тоже считаешь детерминант. также при работе с eigenvalues и eigenvectors тебе тоже без детерминанта не обойтись… хотя здается мне что это слишком сложно))) чтобы тебе объяснять. Спроси у преподавателя. Я когда что-то не понимаю иду спрашиваю у препода, потому что ему за это это платят, чтобы объяснять все это тебе.)))
Ceza Doch Cezarja   27 — 27.11.10 — 13:39	Спасибо огромное!! Всё-таки попытаюсь сама, но если не получится придётся идти к нему)))Великому и Ужасному))
gr13   28 — 27.11.10 — 13:40	20-21 год, психолог, а что в медицинском математику учат?
Ceza Doch Cezarja   29 — 27.11.10 — 13:41	Ага. Видимо для общего развития.
gr13   30 — 27.11.10 — 13:42	сочувствую) на кого учимся, то?
Ceza Doch Cezarja   31 — 27.11.10 — 13:46	Педагог-психолог. По профессии далека от математики)
gr13   32 — 27.11.10 — 13:48	зависит наскольо глубоко ты учишь математику. хотя детерминант матрицы я находил еще в школе, правда не помню в обычном класе или городском
Ceza Doch Cezarja   33 — 27.11.10 — 13:50	Мы их учили в колледже, но… Но.)
gr13   34 — 27.11.10 — 13:55	но все забылось) согласен) я когда-то в училище писал программу по нахождению детерминанта н-мерной матрицы)

TurboConf 5 — расширение возможностей Конфигуратора 1С

ВНИМАНИЕ! Если вы потеряли окно ввода сообщения, нажмите Ctrl-F5 или Ctrl-R или кнопку «Обновить» в браузере.

Ветка сдана в архив. Добавление сообщений невозможно.
Но вы можете создать новую ветку и вам обязательно ответят!
Каждый час на Волшебном форуме бывает более 2000 человек.

Матрицы

История развития

Впервые матрица под названием "волшебный квадрат" упоминается еще в Древнем Китае. Подобные квадраты чуть позже были известны и у арабских математиков. С развитием теории определителей в конце 17 века швейцарский математик Габриэль Крамер (1704 — 1752) начал разрабатывать свою теорию и в 1751 году, не задолго до своей смерти, опубликовал "правило Крамера" — метод решения систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем матрицы системы. В этот же период появился и "метод Гаусса", применяемый для решения СЛАУ и основанный на последовательном исключении неизвестных.

Как отдельная теория, теория матриц получила свое активное развитие в середине 19 века в работах ирландского математика и физика Уильяма Гамильтона (1805 — 1865) и английского математика Артура Кэли (1821 — 1895). Фундаментальные результаты в теории матриц принадлежат также немецким математикам Карлу Вейерштрассу (1815 — 1897), Фердинанду Георгу Фробениусу (1849 — 1917) и французскому математику Мари Энмону Камиль Жордану (1838 — 1922). Современное название "матрица" было введено английским математиком Джеймсом Сильвестром (1814 — 1897) в 1850 году.

Применение матриц

Матрицы широко применяются в математике для компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных.

Матрица (математика)

Матричный аппарат позволяет свести решение СЛАУ к операциям над матрицами.

Матрицей размера 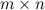называется прямоугольная таблица специального вида, состоящая из строк и столбцов, заполненная некоторыми элементами и ее называют матрицей размера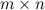 или 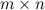-матрицей. Элементы матрицы обозначаются , где 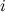— номер строки, в которой находится элемент, а — номер столбца. Количество строк и столбцов матрицы задают ее размеры. Размер матрицы указывается справа внизу возле ее имени, либо таблицы с обозначением элементов.

Для обозначения таблица берется либо в круглые скобки, либо окружается двумя параллельными вертикальными прямыми, например

 

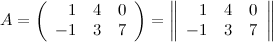
Задание. Чему равен элемент 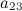матрицы ?

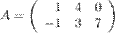Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:

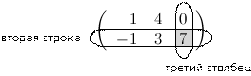
Таким образом, .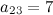

Строка матрицы называется нулевой, если все ее элементы равны нулю. Если хотя бы один из элементов строки не равен нулю, то строка называется ненулевой.

Аналогичное определение и для нулевого и ненулевого столбцов матрицы. Например, в матрице первая строка является нулевой (любой элемент этой строки равен нулю); вторая строка ненулевая, так как элемент .

Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.

Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.

Пример

1 и 6 — элементы главной диагонали.

3 и 4 — элементы побочной диагонали.

 

Для матрицы 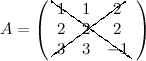элементы 1, 2, -1 образуют главную диагональ; а элементы 3, 2, 2 — побочную.

 

Оглавление:

Основные теоретические сведения

Матрицы

К оглавлению…

Матрицей называют прямоугольную таблицу, заполненную числами. Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами.

Сами числа называют элементами матрицы и характеризуют их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса, причем вначале записывают номер строки, а затем столбца. Например, a₁₄ есть элемент матрицы, стоящий в первой строке и четвертом столбце, a₃₂ стоит в третьей строке и втором столбце.

Главной диагональю квадратной матрицы называют элементы, имеющие одинаковые индексы, то есть те элементы, у которых номер строки совпадает с номером столбца. Побочная диагональ идет «перпендикулярно» главной диагонали.

Особую важность представляют собой так называемые единичные матрицы. Это квадратные матрицы, у которых на главной диагонали стоят 1, а все остальные числа равны 0. Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О.

Простейшие действия с матрицами

1. Умножение матрицы на число. Для этого необходимо умножить каждый элемент матрицы на данное число.

2. Сложение матриц. Складывать можно только матрицы одинакового размера, то есть имеющие одинаковое число строк и одинаковое число столбцов. При сложении матриц соответствующие их элементы складываются.

3. Транспонирование матрицы. При транспонировании у матрицы строки становятся столбцами и наоборот. Полученная матрица называется транспонированной и обозначается A^T. Для транспонирования матриц справедливы следующие свойства:

4. Умножение матриц. Для произведения матриц существуют следующие свойства:

• Умножать можно матрицы, если число столбцов первой матрицы равно числу строк второй матрицы.
• В результате получится матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
• Умножение матриц некоммутативно. Это значит, что от перестановки местами матриц в произведении результат меняется. Более того, если можно посчитать произведение A∙B, это совсем не означает, что можно посчитать произведение B∙A.
• Пусть C = A∙B. Для определения элемента матрицы С, стоящего в i-той строке и k-том столбце необходимо взять i-тую строку первой умножаемой матрицы и k-тый столбец второй. Далее поочередно брать элементы этих строки и столбца и умножать их. Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее.

  А потом все эти произведения надо сложить.

Свойства произведения матриц:

Определитель матрицы

Определителем (детерминантом) квадратной матрицы А называется число, которое обозначается detA, реже |A| или просто Δ, и вычисляется определённым образом. Для матрицы размера 1х1 определителем является сам единственный элемент матрицы.

Примеры решения матриц

Для матрицы размера 2х2 определитель находят по следующей формуле:

Миноры и алгебраические дополнения

Рассмотрим матрицу А. Выберем в ней s строк и s столбцов. Составим квадратную матрицу из элементов, стоящих на пересечении полученных строк и столбцов. Минором матрицы А порядка s называют определитель полученной матрицы.

Рассмотрим квадратную матрицу А. Выберем в ней s строк и s столбцов. Дополнительным минором к минору порядка s называют определитель, составленный из элементов, оставшихся после вычеркивания данных строк и столбцов.

Алгебраическим дополнением к элементу a_ik квадратной матрицы А называют дополнительный минор к этому элементу, умноженный на (–1)^i+k, где i+k есть сумма номеров строки и столбца элемента a_ik. Обозначают алгебраическое дополнение A_ik.

Вычисление определителя матрицы через алгебраические дополнения

Рассмотрим квадратную матрицу А. Для вычисления ее определителя необходимо выбрать любую ее строку или столбец и найти произведения каждого элемента этой строки или столбца на алгебраическое дополнение к нему. А дальше надо просуммировать все эти произведения.

Когда будете считать алгебраические дополнения, не забывайте про множитель (–1)^i+k. Чтобы счет был более простым, выбирайте ту строку или столбец матрицы, который содержит наибольшее число нулей.

Расчет алгебраического дополнения может сводиться к расчету определителя размером более чем 2х2. В этом случае такой расчет также нужно проводить через алгебраические дополнения, и так далее до тех пор, пока алгебраические дополнения, которые нужно будет считать, не станут размером 2х2, после чего воспользоваться формулой выше.

Обратная матрица

К оглавлению…

Рассмотрим квадратную матрицу А. Матрица A^–1 называется обратной к матрице А, если их произведения равны единичной матрице. Обратная матрица существует только для квадратных матриц. Обратная матрица существует, только если матрица А невырождена, то есть ее определитель не равен нулю. В противном случае обратную матрицу посчитать невозможно. Для построения обратной матрицы необходимо:

1. Найти определитель матрицы.
2. Найти алгебраическое дополнение для каждого элемента матрицы.
3. Построить матрицу из алгебраических дополнений и обязательно транспонировать ее. Часто про транспонирование забывают.
4. Разделить полученную матрицу на определитель исходной матрицы.

Таким образом, в случае, если матрица А имеет размер 3х3, обратная к ней матрица имеет вид:

Производная

К оглавлению…

Рассмотрим некоторую функцию f(x), зависящую от аргумента x. Пусть эта функция определена в точке x₀ и некоторой ее окрестности, непрерывна в этой точке и ее окрестностях. Рассмотрим небольшое изменение аргумента функции ∆x. Пусть при этом функция изменилась на ∆f(x). Тогда производной функции в данной точке называется следующее отношение:

Если у функции можно рассчитать производную, то функцию называют дифференцируемой. А саму операцию вычисления производной называют дифференцированием. В математике принято обозначать производную следующим образом:

Все обозначения равнозначны. Допустимо использовать любое. На практике, конечно, никто не считает производную по определению. Все проще. Для начала необходимо запомнить таблицу производных элементарных функций. По определению, все элементарные функции (те функции, которые Вы изучали в школе) дифференцируемы на всей области определения. Затем также нужно освоить правила дифференцирования.

Таблица производных

Правила вычисления производной

Матрицы. Вся теория и задачи с решениями или ответами

К оглавлению…

Производные. Вся теория и задачи с решениями или ответами

К оглавлению…