admin / 31.12.2017
Игра с нулевой суммой
Содержание
- Примеры решений задач по теории игр
- Решения матричных игр онлайн
- Теория игр
- Доклад: Теория игр 6
- Теория игр
- В игре могут сталкиваться интересы двух (игра парная ) или нескольких (игра множественная ) противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалицию, то игра называетсякоалиционной; если таких коалиций две, то игра сводится к парной.
- Решение подобных задач требует полной определенности формулировании их условий (правил игры ), выявления возможных стратегий игроков, возможных выигрышей (проигрыш понимается как отрицательный выигрыш).
- ИГРА С НУЛЕВОЙ СУММОЙ
- 5.2.2. Игра двух лиц с нулевой суммой
- Теория игр с точки зрения инвестиций
ИГРА С НУЛЕВОЙ СУММОЙ
(zero-sum game) Состязание, в котором проигрыш одного игрока равнозначен выигрышу другого. Игры можно разделить на две категории: с нулевой и с ненулевой суммой. Если сумма выигрышей всех игроков остается постоянной при любых вариантах исхода игры, ее относят к категории игр с постоянной суммой. Но поскольку математически выплаты могут быть смещены по шкале, удобнее и нормальнее называть их играми с нулевой суммой. В игре с нулевой суммой при любом варианте ее исхода выигрыш победителя (победителей) всегда равен убытку проигравшего (проигравших). Большинство игр в обычном смысле слова, без избирательного вмешательства извне, являются именно такими играми. К ним принадлежат, в частности, шахматы и футбол (даже если какая-то посторонняя организация присуждает за победу установленную награду). Однако футбольная игра, в которой игрокам платят за то, чтобы они сыграли вничью, или игра в слова (в которой игроки получают очки, составляя слова из случайных разрозненных букв), где награда дается за наибольшую сумму набранных очков, представляют собой примеры игр с нулевой суммой. Такое определение предпочтительнее чем «с положительным результатом» или «с отрицательным результатом». Несмотря на широкое употребление двух последних определений, они обычно создают путаницу, а иногда и оказываются неверными, т.к. не дают точного определения тому, с чем сравнивать положительный результат. В 1944 г. Дж. фон Нейман и О. Моргенштерн выдвинули теорию, согласно которой во всех играх с нулевой суммой и двумя участниками существует особое равновесие, когда каждый участник выбирает стратегию, которая сводит до минимума его потери при любой возможной стратегии противника (см. также: «Минимакс»; «максимин»). Это элегантное математическое построение имеет ограниченное практическое значение, хотя и свидетельствует о существовании оптимальной стратегии игры в шахматы. К счастью, эта стратегия до сих пор не найдена. Игры с нулевой суммой имеют в политике менее формальное значение. Если в игре участвуют два партнера, объединение между ними не возможно; при большем количестве игроков возникают широкие, часто безграничные возможности создания временных коалиций одной части игроков против другой. Поэтому игры с образованием коалиций имеют нулевую сумму. Некоторые авторы причисляют к этой категории и другие политологические игры, например, гонку вооружений или промышленный конфликт. Это неизменно приводит к мрачным прогнозам, поскольку в данных случаях исключается длительное взаимодействие. Игры с ненулевой суммой дают игрокам возможность взаимодействия для получения оптимального результата. Это остается в силе независимо от того, подразумевает игра взаимодействие или нет. Даже в игре без взаимодействия, например в «дилемме заключенных» (prisoners dilemma), игроки имеют возможность размышлять о ходе мыслей противника. В повторяющихся играх без взаимодействия игроки могут координировать свои действия на основе равновесия взаимодействия (более высокого по уровню) (см: суперигра). Большинство политологических игр, кроме игр с образованием коалиций, наверное, лучше всего рассматривать как игры с ненулевой суммой».
Оцените определение:
Источник: Политика. Оксфордский толковый словарь
Примеры решений задач по теории игр
В этом разделе вы найдете бесплатные примеры решений задач по теории игр: нахождение нижней и верхней цены игры, седловой точки, решение игр аналитическим и графическим методом, решение игр сведением к задачам ЛП, решение игр с природой по различным критериям и т.д.
Трудности с задачами? МатБюро поможет: контрольные по теории игр.
Решения матричных игр онлайн
Задача 1. Зная платежную матрицу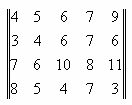
определить нижнюю и верхнюю цены игры и найти решение матричной игры.
Решение матричной игры в чистых стратегиях (pdf, 92 Кб)
Задача 2. Найти стратегии игроков А, В и цену игры, заданной матрицей (с помощью формул и графически)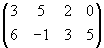
Решение матричной игры аналитически и графически (pdf, 167 Кб)
Задача 3. Найти оптимальный вариант электростанции по критериям Лапласа, Вальда, Гурвица с показателями 0,8 и 0,3 и Сэвиджа по заданной таблице эффективностей (Таблица эффективностей в файле).
Решение игры с природой (pdf, 128 Кб)
Задача 4. Швейное предприятие реализуется свою продукцию через магазин. Сбыт зависит от состояния погоды. В условиях теплой погоды предприятие реализует 1000 костюмов и 2300 платьев, а при прохладной погоде — 1400 костюмов и 700 платьев. Затраты на изготовление одного костюма равны 20, а платья — 5 рублям, цена реализации соответственно равна 40 рублей и 12 рублей. Определить оптимальную стратегию предприятия.
Составление и решение матричной игры (pdf, 46 Кб)
Задача 5. Найти решение и цену игры, заданной следующей платежной матрицей: $$A=\left( \begin{array} \\12& 22\\ 32 &2 \end{array} \right)$$
Решение игры размерности 2*2 аналитическим методом (pdf, 53 Кб)
Задача 6. Выполните доминирование и найдите оптимальное решение и цену игры, заданной матрицей.
Теория игр
$$A=\left( \begin{array} \\1& 2 & 1 & 2\\ 2& 1& 2& 4\\ 3& 3& 2& 2\\ 4& 1& 3& 3\\ \end{array} \right)$$
Решение матричной игры c предварительным доминированием (pdf, 46 Кб)
Задача 7. Дана матрица игры. Привести игру к задаче линейного программирования. Найти решение матричной игры в смешанных стратегиях $$A=\left( \begin{array}\\ 2& 4 & 8& 5\\ 6& 2& 4& 6\\ 3& 2& 5& 4\\ \end{array} \right)$$
Решение игры сведением к задачам линейного программирования (pdf, 58 Кб)
Другие решения по предмету Математические методы в экономике
Доклад: Теория игр 6
Теория игр
Вряд ли можно найти человека, которому удалось в жизни сыграть во все игры, которые есть на свете,- их множество. У каждой свои правила, свои особенности. Хоккей, например, отличается от футбола, домино — от шахмат, шашки — от «крестиков-ноликов», «морской бой» — от игры в слова и т. д.
И все-таки совершенно непохожие игры принципиально — в главном совершенно одинаковы.
В чем их одинаковость? В столкновении интересов. Вася и Петя играют в шахматы. Каждому во что бы то ни стало, хочется выиграть.
На футбольном поле встречаются две команды. Кто-то из них должен стать победителем. Одна, безусловно, приложит к этому все силы. И вторая полона решимости победить.
Столкновение интересов бывает не только в играх. Оно случается часто, намного чаще, чем мы предполагаем. Проследите под этим углом зрения один из своих обычных дней. Сколько раз сталкивались ваши интересы с чьими-либо!
В повседневной жизни, в практической деятельности очень часто встречаются ситуации, когда разные люди проявляют разные интересы и располагают разными путями в достижении разных целей. Иными словами, всем нам часто приходится сталкиваться с конфликтными ситуациями.
Такие ситуации, возникающие при игре в шахматы, шашки, домино и т. д. Результат каждого хода игрока зависит от ответного хода противника, цель игры — выигрыш одного из партнёров. В экономике конфликтные ситуации встречаются очень часто и имеют многообразный характер. К ним относятся, например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Во всех этих примерах конфликтная ситуация порождается различием интересов партнёров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнёра, и учитывать неизвестные заранее решения, которые эти партнёры будут принимать.
Для грамотного решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которая носит название теория игр.
|
Теория игр — математическая дисциплина, устанавливающая количественные закономерности в конфликтных и неопределенных ситуациях. |
Теория игр была разработана Дж. фон Нейманном и О. Моргенштерном в 1944 г., ее дальнейшую разработку продолжил Дж. Нэш.
Ознакомимся с основными понятиями теории игр. Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте, — игроками, а исход конфликта — выигрышем. Для каждой формализованной игры вводятся правила, т.е.
система условий, определяющая: 1) варианты действий игроков; 2) объём информации каждого игрока о поведении партнёров; 3) выигрыш, к которому приводит каждая совокупность действий. Как правило, выигрыш (или проигрыш) может быть задан количественно; например, можно оценить проигрыш нулём, выигрыш — единицей, а ничью — ?..
Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Мы будем рассматривать только парные игры. В них участвуют два игрока А и В, интересы которых противоположны, а под игрой будем понимать ряд действий со стороны А и В.
В теории игр смысл терминов несколько иной. В теории игр игроком могут быть и несколько человек с определенным интересом, которые борются против одного или, наоборот, против большого количества противников, которые тоже признаны игроком. Значит, игрок — это просто одна группа интересов. Футбольный матч с точки зрения теории игр будет просчитываться как один игрок против одного. В этом смысле он не отличается от шахматной партии.
Выдающийся французский математик Луи Борель еще в начале XX века предпринял издание большого, многотомного «Курса теории вероятностей и ее приложений». Предпоследний том был посвящен «Приложениям к азартным играм». Ученый подвел в нем итог своим длительным исследованиям азартных игр, которыми он интересовался как математик. В теорию игр Борель внес смелые и оригинальные идеи. Он попытался найти математическую формулировку игр, когда течение игры зависело от умения игроков. Со временем многие ученые развили теорию. Она стала гораздо шире теории азартных игр.
Оказывается, игры бывают антагонистические и неантагонистические, бабочкообразные и вогнуто-выгнутые, бескоалиционные и кооперативные, позиционные и динамические, и даже игры с «линией жизни», и игра с преследованием с ограниченным временем. Есть в теории игр и «общая теория полезности», и еще много других интересных и необходимых для решения важных практических задач.
В игре могут сталкиваться интересы двух (игра парная ) или нескольких (игра множественная ) противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалицию, то игра называетсякоалиционной; если таких коалиций две, то игра сводится к парной.
Решение подобных задач требует полной определенности формулировании их условий (правил игры ), выявления возможных стратегий игроков, возможных выигрышей (проигрыш понимается как отрицательный выигрыш).
Игра называется игрой с нулевой суммой, или антагонистической, если выигрыш одного из игроков равен проигрышу другого, т. е. для полного задания игры достаточно указать величину одного из них.
Выбор и осуществление одного из предусмотренных правилами действий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход — это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре). Случайный ход — это случайно выбранное действие (например, выбор карты из перетасованной колоды).
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации. Обычно в процессе игры при каждом личном ходе игрок делает выбор в зависимости от конкретной ситуации.
Однако в принципе возможно, что все решения приняты игроком заранее (в ответ на любую сложившуюся ситуацию). Это означает, что игрок выбрал определённую стратегию, которая может быть задана в виде списка правил или программы. (Так можно осуществить игру с помощью ЭВМ). Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной — в противном случае.
А теперь познакомимся со скандальной историей, случившейся в одном из игорных домов Европы.… Сначала на них никто не обращал внимания. Молодые люди заходили в казино поглядеть на игру в рулетку, останавливались возле игорных столов и записывали в блокноты номера выигрышей, то есть номера чисел на диске рулетки, против которых останавливался шарик. «Просто так, любопытства ради»,- отвечали они тому, кто их спрашивал: «Зачем?». А спустя два месяца в Монте-Карло, в столице игорных домов, разразилась гроза. Снова пришли те молодые люди. Но теперь они ничего не записывали, а стали играть. И выигрывали, как говорят математики, «в достаточно длинных партиях».
Журналисты захотели найти объяснение, и считают, что нашли. Оказывается, молодые люди не ради любопытства записывали номера выигрышей. Мало того, они еще их и закодировали. И после этого переслали в Лондон своему компаньону. Тот обработал их с помощью электронной вычислительной машины.
В «американском случае» машинное руководство к действию (алгоритм поиска вариантов) было составлено так, чтобы изыскивать повышение вероятностей благоприятного исхода. Именно с этой целью перебирала машина горы чисел, строя свою игру против вымышленного противника по законам теории игр.
Право же, не стоило создавать целое направление в математике, чтобы помогать выигрывать в азартные игры! Конечно, теория игр создана не для этого
Модели игр служат тем инструментом, с помощью которого теория игр пытается проверить серьезные задачи.
С помощью теории игр стремятся выработать целесообразную линию поведения для многих и многих систем, ведущих борьбу против другой системы.
Например, теорию игр можно применить к задачам связи, к вопросам технологии медицины, нефтедобычи, спорта, рыболовства, к противовоздушной обороне, к задачам, которые приходится решать командиру в сражении. Под углом зрения теории игр можно рассматривать и работу экспериментатора, который составляет план экспериментов. Их можно рассматривать как игру, где противниками выступают ученый и нервная система животного, которую он изучает.
Есть игры, в которых прорабатываются сложные ситуации, растянутые во времени. Для них готовят специальное математическое обеспечение, им нужна достаточно мощная база вычислительных машин.
Ведь для исследования даже самой простой производственно-хозяйственной ситуации бывает необходимым провести большое количество вычислений.
В большинстве случаев в играх приходится иметь дело с цифрами: проделывать головокружительное количество вычислений.
Не случайно, значит, учат машину играть в разные игры: в домино, в шашки, в шахматы.
ИГРА С НУЛЕВОЙ СУММОЙ
Шахматы, дающие астрономическое число вариантов партий -2*10116 — открывают большой простор для исследований.
Теория игр имеет большое значение в экономическом анализе. В последние годы значение теории игр существенно возросло во многих областях экономических и социальных наук. С помощью теории игр предприятие получает возможность предусмотреть ходы своих партнеров и конкурентов.
Эта теория рассматривает поведение фирм на рынке как игру, причем имеются определенные правила игры, по результатам которой начисляются «призы» и «штрафы». Участники игры определенно не знают стратегию конкурента, поэтому их поведение основано лишь на прогнозах.
Например, рассмотрим стратегию фирм А и В (табл. 4) с понижением цены. Если обе фирмы не понижают цену, прибыль каждой составит, например, 60 млн усл. ед. Если одна из фирм понижает цену, она получает конкурентное преимущество и увеличивает прибыль до 85 млн усл. ед. В это время конкурент терпит убыток в размере 25 млн усл. ед. Если же обе фирмы в сговоре проводят политику снижения цены, прибыль каждого составит по 12,5 млн усл. ед. Необходимо определить, как поступить фирмам А и В, чтобы не проиграть.
Аналогом данной ситуации на рынке служит другая игра — так называемая «дилемма заключенного». Суть этой игры в следующем: два узника содержатся в отдельных камерах и обвиняются по одному делу (табл. 5).
У обвинения достаточно улик, чтобы осудить узников только на два года. Узникам сообщили (каждому отдельно), что если один сознается, а другой нет, то сознавшийся будет свободен, а не сознавшийся получит 20 лет. Если сознаются оба, то каждый получит по 10 лет. Необходимо определить, каким будет поведение заключенного, когда реакция другого неизвестна.
В этом случае различают две стратегии поведения, называемые maximin и maximax:
1. min — это стратегия пессимиста.
2. max — это стратегия оптимиста.
Пессимист будет искать наилучший вариант из наихудших результатов. Это ситуация, когда, например, узник А ждет, что узник В признается, и тогда А получит 20 лет заключения, при условии, что он не сознается. Чтобы обеспечить себе наименее плохой результат из всех плохих вариантов, узник А решает сознаться, поскольку это позволит ему получить 10 лет заключения, а не 20. Этот результат лучше, чем 20 лет заключения.
Аналогично будет рассуждать и узник В. В результате, не сговариваясь, оба узника придут к решению сознаться и получат по 10 лет тюрьмы.
Оптимист надеется на самый лучший вариант решения вопроса. Узник А думает, что узник В не сознается, поэтому он решает сознаться. Но узник В также оптимист и поступает аналогичным образом. В результате, не сговариваясь, оба заключенных придут к решению сознаться и получат по 10 лет тюрьмы.
Стратегии min и max привели узников к одному результату — это и есть решение Нэша.
Подобного рода решение примут фирмы А и В на конкурентном рынке. В обоих случаях фирмы А и В решают снижать цены, и стратеги min и max приведут их к решению Нэша, т. е. понижать цены, что даст им равные прибыли — по 12,5 млн усл. ед, каждой фирме.
Заключение
«Есть в современной математике одна область, она носит безобидное название теории игр, но ей, несомненно, суждено сыграть очень важную роль в человековедении самого ближайшего будущего, — говорил Джон фон Нейман, один из основоположников кибернетики.- Она занимается вопросами оптимального поведения людей при наличии противодействующего противника. Для ученого противник — это природа со всеми ее явлениями; экспериментатор борется со средой; математик — с загадками математического мира; инженер — с сопротивлением материалов».
Скачать реферат
Математик Джон Форбс Нэш наверняка известен многим по драме Рона Ховарда «Игры разума», в которой роль гениального математика, страдающего шизофренией, исполнил Рассел Кроу. Но мало кто знает, что исследования, которые прославили Нэша, касались игр с нулевой суммой.
Покер как раз и является игрой с нулевой суммой (если не принимать во внимание рейк), а потому работы Нэша нашли свое применения и в покерной математике. Так получилось, что Нэш, никогда не игравший в покер, стал «отцом» покерной математики.

Равновесием Нэша в покере — такая ситуация, когда изменение стратегии одного из игроков, не может увеличить его выигрыш при неизменности стратегий остальных игроков.
Однако достичь равновесия Нэша в покере практически невозможно, так как выбор решений настолько велик, что даже самые современные компьютеры не способны обрабатывать их. Поэтому о равновесии Нэша говорят в самых простых покерных дисциплинах, таких как гипер-турбо и хедс-ап. Для еще большего упрощения диапазон решений сокращают до пуша или фолда.
Представим теперь, что нам стала известно как со стратегией пушей соперника.
5.2.2. Игра двух лиц с нулевой суммой
Исходя из нее, мы рассчитали оптимальную стратегию коллов. В свою очередь оппонент изменил свою стратегию пушей на оптимальную для спектра наших коллов. Нэш доказал, что рано или поздно возникнет ситуация, когда спектры пуша и колла будут оптимальны друг для друга. То есть если кто-то изменит свою стратегию, то его ожидание понизится. Это и будет равновесием Нэша. На основании работ Нэша были созданы специальные чарты, реализующие стратегию в покере, соответствующую равновесию Нэша в математике покера Читай подробнее здесь.
Таблица 4.2
Представители теории игр
| Представитель | Основной труд |
| Дж. Фон Нейман и О. Моргенштерн | «Теория игр и экономическое поведение», (1944). |
| Джон Форбс Нэш | Основная статья: «Некооперативные игры», 1951. |

Джон Нэш
(1928-)
Джон Нэш — американский математик- экономист, работающий в области теории игр и дифференциальной геометрии. Лауреат Нобелевской премии по экономике 1994 года
«За анализ равновесия в теории некооперативных игр». Известен широкой публике большей частью по биографической драме «Игры разума» (2001) о математическом гении и борьбе с шизофренией.
Вопросы для повторения

Джон Нейман
(1903-1957)
1) Опишите алгоритм поиска нерациональных стратегий. Может ли игрок иметь несколько нерациональных стратегий? Может ли он не иметь их вовсе?
2) Опишите алгоритм поиска осторожных стратегий. Может ли игрок иметь
несколько осторожных стратегий? Может ли он не иметь их вовсе?
3) Опишите алгоритм поиска равновесных стратегий.
4) С какой целью институциональный человек отклоняется от равновесной стратегии?
Рекомендуемая литература
1) Биета, Ф. Теория игр и финансовые рынки / Ф. Биета, П. Смилянец //
Вопросы экономики. – 2007. — №10. — С. 114-124.
2) Корнейчук, Б. В. Институциональная экономика / Б. В.
Теория игр с точки зрения инвестиций
Корнейчук. – М.: Гардарики, 2007. – 255 с.
3) Майерсон, Р. Равновесие по Нэшу и история экономической науки / Р. Майерсон // Вопросы экономики. – 2010. — № 6. — С. 26-43.
⇐ Предыдущая23242526272829303132Следующая ⇒
Дата публикования: 2014-12-25; Прочитано: 212 | Нарушение авторского права страницы

FILED UNDER : IT