admin / 21.12.2017
пилообразный сигнал — это… Что такое пилообразный сигнал?
гармоническая составляющая, период которой равен периоду негармонического сигнала, называется первой или основной гармоникой сигнала. Все остальные составляющие называются высшими гармоническими составляющими. Гармоника, частота которой в k раз больше первой гармоники (а период, соответственно, в k раз меньше) , называется k — ой гармоникой.
Гармоники УКВ ЧМ (FM) передатчиков лежат далеко за пределами вещательного диапазона 87,5 — 108 МГц. К примеру. Вторая гармоника, это частоты от 175 до 216 МГц, Третья гармоника — от 262,5 до 324 МГц. И так далее, по формуле (87,5 …108) х N Где N — номер гармоники.
по-русски — это повторение сигнала (возможно и неоднократное) выше или ниже основной частоты передачи. связано с особенностями преобразования сигнала с применением ПЧ — промежуточных частот. Допустим, модулируется сигнал частотой в 1 мГц и промежуточная 565 кГц. На выходе образуются уже 2 частоты: 1565 кГц (верхняя) и 445 кГц (нижняя) . Нижнюю давим, верхнюю излучаем. плохо давим — будут слышны обе. ПЧ может быть и двойное и тройное, соотв-но и гармоник — до хрена, они еще между собой складываются и в приемнике свист и вой.. .
Любую функцию можно представить в виде суммы членов бесконечной последовательности. Каджый n-ный член такой последовательности представляет собой уравнение синусоидальной функции, и называется n-ной гармоникой (или по простому — составляющей).
В математике есть такое направление-гармонический анализ. Базируется он на теореме Фурье-согласно которой, любую периодическую функцию можно представить в виде суммы гармонических (синусоидальных) функций кратного периода. Т. е. любой периодический сигнал представляется суммой синусоидальных сигналов различной амплитуды и частотой кратной основной (больше в 2,3,4….n) раз. Эти сигналы и называются гармониками. Когда говорят о наличии гармоник, это значит что форма сигнала отличается от синусоиды.
Войдите, чтобы написать ответ
Содержание
Пилообразный сигнал
Cтраница 1
Пилообразный сигнал доходит до напряжения 2 / 3UKK, затем быстро спадает ( разряд происходит через внутренний разряжающий и-р-и-транзистор схемы 555, контакт 7) до напряжения 1 / 3UKK, далее цикл начинается снова. Отметим, что этот сигнал пилообразной формы выделяется на выводе конденсатора и необходимо обеспечить его развязку с помощью ОУ, который обладает высоким полным сопротивлением. [2]
Пилообразный сигнал задерживающего генератора, поступая на компаратор, позволяет устанавливать необходимую задержку развертки, изменяя опорное напряжение. Регулируя задержку, совмещают границы измеряемого участка осциллограммы с удобной вертикальной линией шкалы, фиксируя по шкале регулятора опорного напряжения мгновенные значения напряжения пилообразного сигнала задерживающего генератора, которые соответствуют началу ( D) и концу ( t / 2) измеряемого участка осциллограммы. [4]
Осциллограмма периодического пилообразного сигнала s ( t) приведена на рис. 1.2.5. Получите выражения для коэффициентов Сп комплексного ряда Фурье. [5]
Генератор вырабатывает непрерывные положительные пилообразные сигналы с диапазоном частот от 15 гц до 300 кгц. Диапазон триггерных частот составляет 25 гц 50 кгц; длительность развертки 10 — -, н — 10 000 мксек. Триггерные импульсы имеют максимальную амплитуду 35 в пикового значения с положительной или отрицательной полярностью.
Амплитудный спектр сигнала. Амплитудно-частотная характеристика (АЧХ).
[6]
Он генерирует непрерывные и пусковые пилообразные сигналы и выдает отметки амплитуды и времени, обеспечивая тем самым проведение разнообразных испытаний и измерений, выходящих за пределы обычной области применения осциллографов. [7]
Поскольку размах пилообразного сигнала неизменен при любом значении Тп, то значениям 0ЗГП и 0 8ГП соответствуют одни и те же значения иц. Сигнал на выходе компаратора возникает в том случае, если мгновенное значение пилообразного напряжения превышает опорный уровень. Контрольные импульсы с выхода компараторов поступают на две логические ячейки И. Измерительный импульс с устройства синхронизации подается на те же ячейки. В зависимости от его длительности на выходах ячеек И могут быть либо единичные, либо нулевые сигналы. Эти сигналы поступают на два триггера, которые осуществляют хранение полученной информации. [8]
Генератор должен вырабатывать пилообразные сигналы с крутизной 10 в / сек и длительностью 10 мксек. Напряжения источников питания составляют 300 в и — 200 я, а частота повторения пилообразного напряжения должна быть равна 1 кгц. [9]
Принято, что пилообразный сигнал в каждом периоде начинается с нуля в момент прихода очередного тактового импульса. [11]
Повторите эксперимент, заменив синусоиду на пилообразный сигнал, а также на прямоугольные импульсы. [12]
Когда на вход усилителя Л поступает пилообразный сигнал генератора Б, уровень напряжения на выходе транзистора ТЗ низкий, диоды ДЮ и Д12 проводят, потенциал на их анодах, а следовательно, и на затворах полевых транзисторов Т4 и Т5 примерно равен 0 5 В. [14]
Этот частотный спектр немногим лучше спектра пилообразного сигнала ( с сигналами такого вида встречаются в электронике), сравниться с которым по шум-ности не может ни один двигатель, даже созданный самым злонамеренным проектировщиком. [15]
Страницы: 1 2 3 4 5

Если сигнал периодический с частотой следования f, то частоты, составляющие этот сигнал, кратны f, то есть f, 2f, 3f, 4f и т.д.
что такое гармоника сигнала???
Эти частоты называются гармониками. Первая гармоника есть f, вторая гармоника — 2f, третья гармоника — 3f, и так далее. Первую гармонику, f, часто называют основной частотой (fundamental frequency).
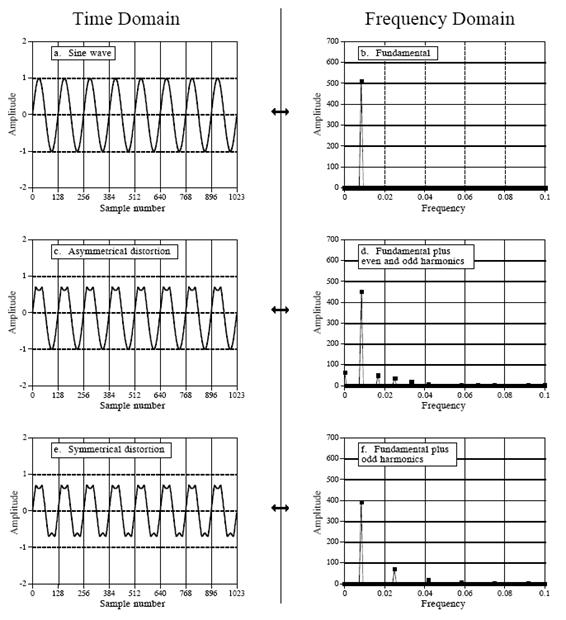
РИСУНОК 11-7
Пример гармоник. Ассиметричное искажение, показанное в (с), вызывают четные и нечетные гармоники (d), Симметричные искажения, показанные в (е), приводят только к четным гармоникам (f).
На рисунке 11-7 показан пример гармоник. Рисунок (а) чистая синусоида, (b) – ее ДПФ, одиночный пик. В (с) синусоида искажена в верхней части. В (d) показан результат этого искажения в частотной области. Так как искаженный сигнал периодический с той же самой частотой, как и исходный, частотная область состоит из того же пика плюс гармоники. Гармоники могут быть любой амплитуды, однако они обычно становятся меньше с увеличением их частоты. Как и для любого сигнала, резкие края приводят к высоким частотам. Например, рассмотрим обычный генератор квадратных волн частотой 1 кГц на элементах ТТЛ логики. Резкий подъем за несколько наносекунд даст гармоники около 100 МГц, десять тысяч гармоник!
Рисунок (е) демонстрирует тонкий гармонический анализ. Если сигнал симметричен относительно горизонтальной оси, то есть верхние лепестки есть зеркальное отражение нижних лепестков, то все четные гармоники будут равны нулю. Как показано в (f), сигнал состоит из основной частоты, третьей гармоники, пятой гармоники и т.д.
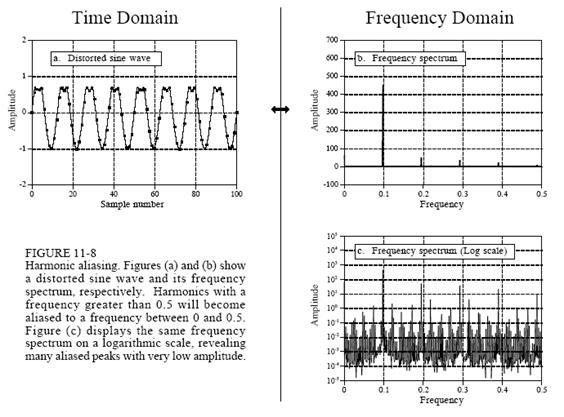
РИСУНОК 11-8
Наложение гармоник. Рисунки (а) и (b) показывают искажение синусной волны и ее частотный спектр, соответственно. Гармоник выше, чем 0,5, будут накладываться между 0 и 0,5. Рисунок (с) показывает частотный спектр в логарифмическом масштабе, вскрывая множество пиков наложения с очень маленькой амплитудой.
Все непрерывные периодические сигналы могут быть представлены суммой гармоник, как было описано. Дискретные периодические сигналы имеют проблему, которая нарушает это простое отношение. Как вы, возможно, догадались проблема в наложении. Рисунок 11-8а показывает синусную волну, искаженную в верхней части так же, как был искажен предыдущий сигнал. Этот сигнал выглядит менее регулярным и сглаженным чем в предыдущем примере, поскольку синусная волна имеет много более высокую частоту, что дает всего несколько отсчетов на цикл. Рисунок (b) показывает частотный спектр этого сигнала. Как и ожидается, вы можете определить основную частоту и гармоники. Этот пример показывает, что гармоники могут простираться до частот много больше, чем 0,5 частоты дискретизации, и накладываться между 0 и 0,5. Вы не заметите их в (b) потому, что амплитуды их слишком малы. Рисунок (с) показывает частотный спектр в логарифмическом масштабе, демонстрируя наложение этих малых пиков. На первый взгляд этот спектр выглядит похожим на случайный шум. Но это не так, это результат перекрытия многих гармоник при их наложении.
Важно понимать, что этот пример предполагает искажение сигнала после того, как он был представлен в цифровом виде. Если это искажение происходит с аналоговым сигналом, вы можете удалить ненужные гармоники антиэлайзинговым фильтром перед оцифровкой.
Гармоники наложения являются проблемой только тогда, когда нелинейные операции выполняются непосредственно над дискретным сигналом. Даже в этом случае амплитуда этих гармоник наложения достаточно мала, и их можно игнорировать.
Концепция гармоник так же полезна по другой причине: она объясняет, почему ДПФ рассматривает временную и частотную области как периодические. В частотной области N-точечное ДПФ состоит из N/2+1 равномерно расположенных частот. Вы можете рассматривать частоты между этими отсчетами как (1) имеющими нулевую величину или (2) не существующими. В любом случае они не вносят вклад в синтез сигнала временной области. Другими словами, дискретный частотный спектр состоит из гармоник, а не из непрерывного уровня частот. Это требует, что бы сигнал временной области был периодический с частотой равной самой низкой частоте из синусоид в частотной области, то есть основной частоте. Пренебрегая величиной постоянного тока (DC), самая низкая частота, представленная в частотной области, делает один полный цикл колебаний каждые N отсчетов, что делает период временной области равной N. Другими словами, если одна область дискретная, другая должна быть периодической, и наоборот. Это имеет силу для всех четырех членов семейства преобразования Фурье. Поскольку ДПФ рассматривает обе области как дискретные, то их необходимо рассматривать и как периодические.
Отсчеты в каждой области представляют гармоники периода противоположной области.
Прямоугольный сигнал
Cтраница 1
Прямоугольные сигналы с выхода триггера подаются на усилительную приставку, которая представляет собой трехкаскадный усилитель на полупроводниковых триодах. В коллектор выходного триода непосредственно включаются электромагниты исполнительных устройств. [1]
Прямоугольный сигнал управляет двумя преобразователями, включенными в противофазе. [2]
Прямоугольный сигнал с максимальной величиной а на входе ограничителя дает на выходе прямоугольный же сигнал с максимальной величиной с. Следовательно, коэффициент усиления равен с / а, если это число меньше единицы, и равен единице, если а меньше с.
Гармонический сигнал
При этом постоянная составляющая отсутствует. [3]
Прямоугольным сигналом можно проверить усилитель покаскадно и снять общую характеристику. Этот метод быстрее других, так как испытания проводятся только на двух частотах. Он более чувствителен к небольшим изменениям в характеристиках, легко обнаруживает фон, моторные шумы или паразитную модуляцию, позволяет легко налаживать компенсирующие цепи и проверять работу регуляторов тембра. Но проверка этим методом носит только приближенный качественный характер без определения количественных соотношений. [4]
На низкочастотный прямоугольный сигнал накладываются остроконечные импульсы или выбросы напряжения, т.е. возникают высшие гармоники, которые обусловливают появление помех. Если же мы рассмотрим диаграмму на рис. 4.5, то можно сделать вывод о том, что емкость триммера занижена. В этом случае происходит интегрирование сигнала или заваливание передних фронтов импульсов. [6]
Помимо импульсного прямоугольного сигнала, имеющего определенную длительность, существуют сигналы в виде скачков и пиков. В первом случае используется лишь часть импульсного сигнала ( один перепад напряжения), а во втором — импульс малой длительности с относительно пологими фронтами. Прямоугольные импульсы и перепады напряжения широко используются в цифровой электронике. В цифровом электронном устройстве информация обрабатывается и передается в виде определенных ( высокого и низкого) логических уровней, которые определяются заранее известными величинами напряжений. [7]
Импульсы и прямоугольные сигналы широко используются в цифровой электронике. В цифровой схеме состояние любой точки в любой момент времени определяют заранее известные уровни напряжения. Эти уровни называют просто ВЫСО-КИЙ и НИЗКИЙ. Они соответствуют значениям ложь ( 0) и истина ( 1) булевой алгебры логики, которая имеет дело с переменными, принимающими эти значения. [8]
ГУН вырабатывает прямоугольный сигнал. Управляющее напряжение, поступающее с выхода интегратора, поддерживает период выходного сигнала ГУН равным 2Туз / 16, где Туз — время распространения ультразвука через продуктопровод. [9]
Импульсы и прямоугольные сигналы широко используются в цифровой электронике. В цифровой схеме состояние любой точки в любой момент времени определяют заранее известные уровни напряжения. Эти уровни называют просто высокий и низкий. Они соответствуют значениям ложь ( 0) и истина ( 1) булевой алгебры логики, которая имеет дело с переменными, принимающими эти значения. [10]
Основная частота прямоугольного сигнала должна быть равна ( или несколько ниже) самой низкой частоты диапазона усилителя. Например, частота 50 гц может использоваться для контроля диапазона от 50 до 5 000 гц. [12]
Скругление формы прямоугольных сигналов, создаваемых телеграфным аппаратом, осуществляется включением в цепь постоянного тока простых нч фильтров. [14]
Амплитудный модулятор прямоугольного сигнала ( рис. 7.16) работает в широком диапазоне частот. Сигнал с модулирующей частотой поступает в базу транзистора VT1, работающего в линейном режиме. Транзисторы VT2 и VT3 работают в дискретном режиме и переключаются с частотой несущего сигнала. [15]
Страницы: 1 2 3 4

Классификация сигналов
РАДИОТЕХНИЧЕСКИЕ СИГНАЛЫ
Информация – не материя и не энергия, поэтому для ее фиксации и передачи необходим материальный носитель – агент. Информация принудительно изменяет агент – модулирует его, после чего он становится материальным носителем информации – сообщением, сигналом. Таким образом, сигнал s(t) – процесс изменения во времени физического состояния какого-либо агента. В радиоэлектронике агентом служат электрические процессы и электромагнитные волны.
Сигналы, применяемые в радиоэлектронике, весьма разнообразны. Их разновидности можно классифицировать по следующим признакам.
1. По предсказуемости мгновенных значений в любые моменты времени различают сигналы детерминированные и случайные. У детерминированных сигналов мгновенные значения предсказуемы точно, т.е. значение сигнала в любой момент времени наперед известно. Мгновенное значение случайного сигнала предсказуемо с некоторой вероятностью.
2. По роли в передаче информации сигналы разделяются на полезные, те, которые несут интересующую нас информацию, и мешающие (шумовые помехи, сигналы несущие другую информацию).
3.По форме описания выделяют аналоговые и дискретные сигналы. Непрерывные (аналоговые) сигналы это те сигналы, которые описываются непрерывной функцией в заданном интервале изменения их мгновенных значений. Дискретными сигналами называются сигналы, которые принимают определенные значения в некоторые фиксированные моменты времени с некоторым шагом дискретизации.
Особую разновидность дискретных сигналов представляют цифровые сигналы. Они характеризуются тем, что каждому из множества взятых в фиксированные моменты времени с некоторым шагом дискретизации отсчетных значений аналогового сигнала ставится в соответствие число с ограниченным количеством разрядов.
Сигналы, которые описываются тригонометрическими функциями 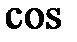 или
или 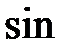 называются гармоническими.
называются гармоническими.
Ci-Bi.com Форум любительской радиосвязи
Гармонический сигнал можно представить в виде
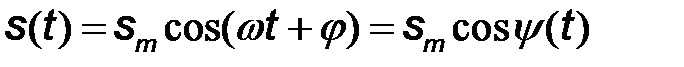 ,
,
где 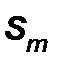 – амплитуда;
– амплитуда; 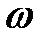 – круговая частота;
– круговая частота; 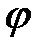 – начальная фаза;
– начальная фаза; 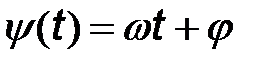 – полная фаза (фазовый угол). Круговая частота
– полная фаза (фазовый угол). Круговая частота 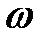 связана с циклической частотой
связана с циклической частотой 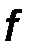 и периодом колебания
и периодом колебания 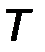 соотношением
соотношением 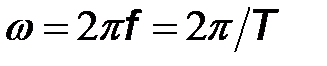 .
.
Гармонические сигналы обладают замечательным свойством: результирующее колебание при линейных операциях – алгебраическом сложении любого числа гармонических колебаний одинаковой частоты, дифференцировании, интегрировании – есть гармоническое колебание той же частоты. Это свойство объясняет широкое применение гармонических сигналов в измерительной аппаратуре в качестве тестовых.
Техника определения параметров результирующего колебания значительно упрощается, если при описании гармонического сигнала вещественную тригонометрическую функцию заменить комплекснозначной экспоненциальной функцией. Вещественному сигналу ставится в соответствие комплексный сигнал:
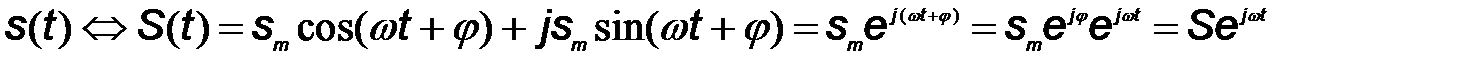 ,
,
где 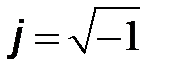 – мнимая единица;
– мнимая единица; 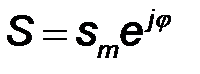 – комплексная амплитуда колебания. Она содержит информацию об амплитуде колебания и о его начальной фазе. Множитель
– комплексная амплитуда колебания. Она содержит информацию об амплитуде колебания и о его начальной фазе. Множитель 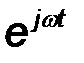 описывает временную зависимость колебания.
описывает временную зависимость колебания.
Поскольку при всех линейных операциях частота гармонического сигнала сохраняется и всегда известна, то остается анализировать только изменения, которые претерпевают амплитуда и фаза сигнала.
Для наглядности часто мгновенные значения комплексных амплитуд сигналов и результат их линейного преобразования изображают векторами на комплексной плоскости. Такое представление называется векторной диаграммой.
Представление гармонического сигнала в комплексной форме составляет основу метода комплексных амплитуд, который широко используется в радиотехнике и электротехнике при анализе линейных цепей.
⇐ Предыдущая123456789Следующая ⇒
Дата добавления: 2014-11-16; Просмотров: 2288; Нарушение авторских прав?;
Читайте также:
FILED UNDER : IT