Алгоритм открытого распределения ключей Диффи-Хеллмана

Предыдущая49505152535455565758596061626364Следующая

 

Алгоритм Диффи-Хеллмана был первым алгоритмом с открытыми ключами (предложен в 1976 г.). Его безопасность обусловлена трудностью вычисления дискретных логарифмов в конечном поле, в отличие от легкости дискретного возведения в степень в том же конечном поле.

 

Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал.

 

1. Обе стороны заранее уславливаются о модуле N (N должен быть простым числом) и примитивном элементе gеZ_N, (1<g<N-1), который образует все ненулевые элементы множества Z_N, т.е. {g.g²…..g^N-1=i}=z_N-{0}.

Эти два целых числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.

 

2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи к_А и к_в (к_А и к_в-случайные большие целые числа, которые хранятся пользователями А и В в секрете).

3. Далее пользователь А вычисляет открытый ключ

 

у_А = g^kA(mod N), а пользователь В — открытый ключ Ув = g^kB(mod N).

 

4. Затем стороны А и В обмениваются вычисленными значениями открытых ключей у_А и у_в по незащищенному каналу. (Мы считаем, что все данные, передаваемые по незащищенному каналу связи, могут быть перехвачены злоумышленником.)

5. Далее пользователи А и В вычисляют общий секретный ключ, используя следующие сравнения:

 

пользователь А: К = (у_в)^kа= (g^kв)^kа (mod N);

 

пользователь В: К’= (у_А)^кв = (g^kа )^kв(mod N).

 

При этом К=К’, так как (g^kв)^kа= (д^kа)^kв (mod N).

 

Схема реализации алгоритма Диффи-Хеллмана показана на рис. 7.5. Ключ К может использоваться в качестве общего секретного ключа

 

(ключа шифрования ключей) в симметричной криптосистеме.

 

Кроме того, обе стороны А и В могут шифровать сообщения, используя следующее преобразование шифрования (типа RSA): C = E_K(M) = М^k(modN).

 

 

 

Рисунок 7.5 – Схема реализации алгоритма Диффи-Хеллмана

 

Для выполнения расшифрования получатель сначала находит ключ расшифрования К* с помощью сравнения

 

K*K*=1(modN-1),

 

а затем восстанавливает сообщение М = D_K (С) = C^K‘(mod N).

 

Пример. Допустим, модуль N=47 а примитивный элемент д = 23. Предположим, что пользователи А и В выбрали свои секретные ключи: kA=12(mod47) и k_B=33(mod47).

 

Для того чтобы иметь общий секретный ключ К, они вычисляют сначала значения частных открытых ключей:

 

y_A = g^kа=23¹² = 27(mod47), y_B = g^kB=23³³=33(mod47).

После того, как пользователи А и В обменяются своими значениями у_А и у_в, они вычисляют общий секретный ключ

 

К = (y_s)^kA = (у_А)^кв = ЗЗ¹² = 27^м = 23¹²"³³ = 25 (mod 47).

 

Кроме того, они находят секретный ключ расшифрования, используя следующее сравнение:

 

K*K*=1(modN-1), откуда К*=35 (mod 46).

 

Теперь, если сообщение М =16, то криптограмма

 

C=M^K=16²⁵ = 21(mod47}. Получатель восстанавливает сообщение так: M = C^K‘ = 21³⁹=16(mod47).

 

Злоумышленник, перехватив значения N, g, у_А и у_в, тоже хотел бы определить значение ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения k_A no N, g, у_А, что g^kAmodN = y_A (поскольку в этом случае, вычислив к_А, можно найти K = (y_B)^kAmodN). Однако нахождение k_A no N,g и у_А-задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.

 

Выбор значений N ид может иметь существенное влияние на безопасность этой системы. Модуль N должен быть большим и простым числом. Число (N-1)/2 также должно быть простым числом. Число g желательно выбирать таким, чтобы оно было примитивным элементом множества Z_N. (В принципе достаточно, чтобы число g генерировало большую подгруппу мультипликативной группы по mod N).

 

Алгоритм открытого распределения ключей Диффи-Хеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи, которой подписываются сообщения об открытом ключе.

 

Метод Диффи-Хеллмана дает возможность шифровать данные при каждом сеансе связи на новых ключах. Это позволяет не хранить секреты на дискетах или других носителях. Не следует забывать, что любое хранение секретов повышает вероятность попадания их в руки конкурентов или противника.

 

Преимущество метода Диффи-Хеллмана по сравнению с методом RSA заключается в том, что формирование общего секретного ключа происходит в сотни раз быстрее. В системе RSA генерация новых секретных и открытых

 

ключей основана на генерации новых простых чисел, что занимает много времени.

 

Предыдущая49505152535455565758596061626364Следующая

Date: 2015-06-06; view: 321; Нарушение авторских прав

Понравилась страница? Лайкни для друзей:

Алгоритм открытого распределения ключей Диффи-Хеллмана

Предыдущая49505152535455565758596061626364Следующая

 

Алгоритм Диффи-Хеллмана был первым алгоритмом с открытыми ключами (предложен в 1976 г.). Его безопасность обусловлена трудностью вычисления дискретных логарифмов в конечном поле, в отличие от легкости дискретного возведения в степень в том же конечном поле.

 

Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал.

 

1. Обе стороны заранее уславливаются о модуле N (N должен быть простым числом) и примитивном элементе gеZ_N, (1<g<N-1), который образует все ненулевые элементы множества Z_N, т.е. {g.g²…..g^N-1=i}=z_N-{0}.

Эти два целых числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.

 

2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи к_А и к_в (к_А и к_в-случайные большие целые числа, которые хранятся пользователями А и В в секрете).

3. Далее пользователь А вычисляет открытый ключ

 

у_А = g^kA(mod N), а пользователь В — открытый ключ Ув = g^kB(mod N).

 

4. Затем стороны А и В обмениваются вычисленными значениями открытых ключей у_А и у_в по незащищенному каналу. (Мы считаем, что все данные, передаваемые по незащищенному каналу связи, могут быть перехвачены злоумышленником.)

5. Далее пользователи А и В вычисляют общий секретный ключ, используя следующие сравнения:

 

пользователь А: К = (у_в)^kа= (g^kв)^kа (mod N);

 

пользователь В: К’= (у_А)^кв = (g^kа )^kв(mod N).

 

При этом К=К’, так как (g^kв)^kа= (д^kа)^kв (mod N).

 

Схема реализации алгоритма Диффи-Хеллмана показана на рис.

7.5. Ключ К может использоваться в качестве общего секретного ключа

 

(ключа шифрования ключей) в симметричной криптосистеме.

 

Кроме того, обе стороны А и В могут шифровать сообщения, используя следующее преобразование шифрования (типа RSA): C = E_K(M) = М^k(modN).

 

 

 

Рисунок 7.5 – Схема реализации алгоритма Диффи-Хеллмана

 

Для выполнения расшифрования получатель сначала находит ключ расшифрования К* с помощью сравнения

 

K*K*=1(modN-1),

 

а затем восстанавливает сообщение М = D_K (С) = C^K‘(mod N).

 

Пример.

РАСШИРЕННЫЙ АЛГОРИТМ ДИФФИ-ХЕЛЛМАНА

Допустим, модуль N=47 а примитивный элемент д = 23. Предположим, что пользователи А и В выбрали свои секретные ключи: kA=12(mod47) и k_B=33(mod47).

 

Для того чтобы иметь общий секретный ключ К, они вычисляют сначала значения частных открытых ключей:

 

y_A = g^kа=23¹² = 27(mod47), y_B = g^kB=23³³=33(mod47).

После того, как пользователи А и В обменяются своими значениями у_А и у_в, они вычисляют общий секретный ключ

 

К = (y_s)^kA = (у_А)^кв = ЗЗ¹² = 27^м = 23¹²"³³ = 25 (mod 47).

 

Кроме того, они находят секретный ключ расшифрования, используя следующее сравнение:

 

K*K*=1(modN-1), откуда К*=35 (mod 46).

 

Теперь, если сообщение М =16, то криптограмма

 

C=M^K=16²⁵ = 21(mod47}. Получатель восстанавливает сообщение так: M = C^K‘ = 21³⁹=16(mod47).

 

Злоумышленник, перехватив значения N, g, у_А и у_в, тоже хотел бы определить значение ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения k_A no N, g, у_А, что g^kAmodN = y_A (поскольку в этом случае, вычислив к_А, можно найти K = (y_B)^kAmodN). Однако нахождение k_A no N,g и у_А-задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.

 

Выбор значений N ид может иметь существенное влияние на безопасность этой системы. Модуль N должен быть большим и простым числом. Число (N-1)/2 также должно быть простым числом. Число g желательно выбирать таким, чтобы оно было примитивным элементом множества Z_N. (В принципе достаточно, чтобы число g генерировало большую подгруппу мультипликативной группы по mod N).

 

Алгоритм открытого распределения ключей Диффи-Хеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи, которой подписываются сообщения об открытом ключе.

 

Метод Диффи-Хеллмана дает возможность шифровать данные при каждом сеансе связи на новых ключах. Это позволяет не хранить секреты на дискетах или других носителях. Не следует забывать, что любое хранение секретов повышает вероятность попадания их в руки конкурентов или противника.

 

Преимущество метода Диффи-Хеллмана по сравнению с методом RSA заключается в том, что формирование общего секретного ключа происходит в сотни раз быстрее. В системе RSA генерация новых секретных и открытых

 

ключей основана на генерации новых простых чисел, что занимает много времени.

 

Предыдущая49505152535455565758596061626364Следующая

Date: 2015-06-06; view: 323; Нарушение авторских прав

Понравилась страница? Лайкни для друзей:

 

Метод открытого распределения ключей позволяет пользователям обмениваться ключами по незащищенным каналам связи.

Криптографические алгоритмы с открытым ключом и их использование

Его безопасность обусловлена трудностью вычисления дискретных логарифмов в конечном поле, в отличие от легкости решения прямой задачи дискретного возведения в степень в том же конечном поле. Суть метода Диффи-Хеллмана заключается в следующем (рис. 4.26).

Пользователи А и В, участвующие в обмене информацией, генерируют независимо друг от друга свои случайные секретные ключи k_Aи k_B (ключи k_Aи k_B – случайные большие целые числа, которые хранятся пользователями А и В в секрете).

Затем пользователь А вычисляет на основании своего секретного ключа k_A открытый ключ

 

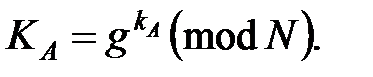(4.39)

 

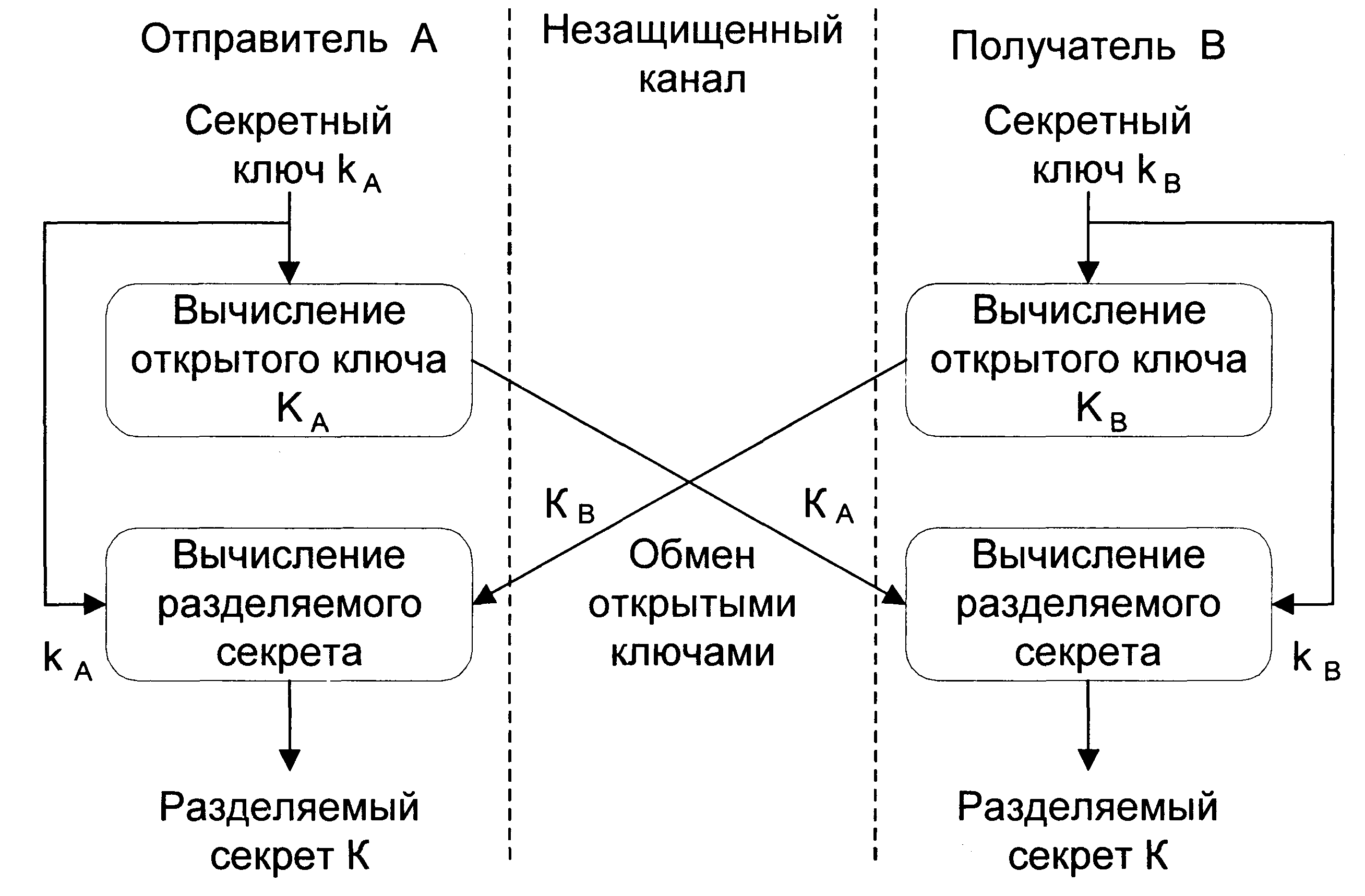
Рис.

4.26. Схема распределения ключей Диффи-Хеллмана

 

Одновременно пользователь В вычисляет на основании своего секретного ключа k_B открытый ключ

 

(4.40)

 

где N и g – большие целые простые числа. Арифметические действия выполняются с приведением по модулю N. Числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей сети или системы.

Затем пользователи А и В обмениваются своими открытыми ключами К_Аи К_B по незащищенному каналу и используют их для вычисления общего сессионного ключа К (разделяемого секрета):

·пользователь А: ;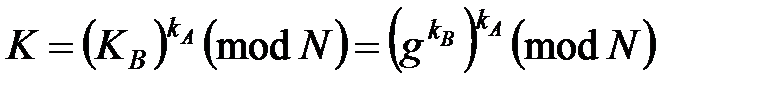

· пользователь B: ;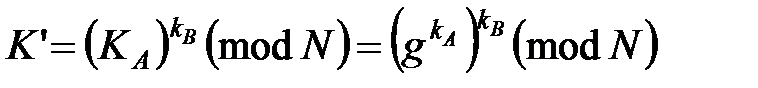

· при этом 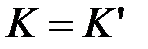, так как .

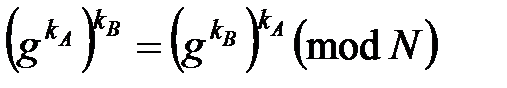Таким образом, результатом этих действий оказывается общий сессионный ключ, который является функцией обоих секретных ключей – k_Aи k_B.

Злоумышленник, перехвативший значения открытых ключей К_Аи К_B, не мо­жет вычислить сессионный ключ К, потому что он не имеет соответствующих значений секретных ключей k_Aи k_B. Благодаря использованию однонаправленной функции операция вычисления открытого ключа необратима, то есть невозможно по значению открытого ключа абонента вычислить его секретный ключ.

Уникальность метода Диффи-Хеллмана заключается в том, что пара абонентов имеет возможность получить известное только им секретное число, передавая по открытой сети открытые ключи. После этого абоненты могут приступить к защите передаваемой информации уже известным проверенным способом – применяя симметричное шифрование с использованием полученного разделяемого секрета.

Схема Диффи-Хеллмана дает возможность шифровать данные при каждом сеансе связи на новых ключах. Это позволяет не хранить секреты на дискетах или других носителях.

Схема Диффи-Хеллмана позволяет реализовать метод комплексной защиты конфиденциальности и аутентичности передаваемых данных. Эта схема предоставляет пользователям возможность сформировать и использовать одни и те же ключи для выполнения цифровой подписи и симметричного шифрования передаваемых данных.

 

Метод комплексной защиты конфиденциальности и аутентичности передаваемых данных

 

Для одновременной защиты целостности и конфиденциальности данных целесообразно применять шифрование и электронную цифровую подпись в комплексе. Промежуточные результаты работы схемы Диффи-Хеллмана могут быть использованы в качестве исходных данных для реализации метода комплексной защиты целостности и конфиденциальности передаваемых данных.

Согласно данному алгоритму пользователи А и В сначала генерируют свои секретные ключи k_Aи k_B и вычисляют свои открытые ключи К_Аи К_B. Затем абоненты А и В используют эти промежуточные результаты для одновременного вычисления общего разделяемого секретного ключа К, который может использоваться для симметричного шифрования данных.

Метод комплексной защиты конфиденциальности и аутентичности передаваемых данных работает по следующей схеме:

· абонент А подписывает сообщение М с помощью своего секретного ключа k_A, используя стандартный алгоритм цифровой подписи;

· абонент А вычисляет совместно разделяемый секретный ключ К по алгоритму Диффи-Хеллмана из своего секретного ключа k_A и открытого ключа К_B абонента В;

· абонент А зашифровывает сообщение М на полученном совместно разделяемом секретном ключе К, используя согласованный с партнером по обмену алгоритм симметричного шифрования;

· абонент В при получении зашифрованного сообщения М вычисляет по алгоритму Диффи-Хеллмана совместно разделяемый секретный ключ К из своего секретного ключа k_B и открытого ключа К_А абонента А;

· абонент В расшифровывает полученное сообщение М на ключе К;

· абонент В проверяет подпись расшифрованного сообщения М с помощью открытого ключа абонента К_А.

На основе схемы Диффи-Хеллмана функционируют протоколы управления криптоключами SKIP (Simple Key management for Internet Protocols) и IKE (Internet Key Exchange), применяемые при построении защищенных виртуальных сетей VPN на сетевом уровне.